Discrete Mathematics

Summary notes

Proofs, Numbers, and Sets

• Lecture notes
• Slides and topics
    Michaelmas term
      1.1 introduction; proof.
      1.2 implication; contrapositive; modus ponens.
      1.3 bi-implication; divisibility; congruence.
         
      2.1 universal quantification.
      2.2 equality.
      2.3 conjunction.
         
      3.1 existential quantification.
      3.2 disjunction.
         
      4.1 Fermat's Little Theorem.
      4.2 negation; contrapositive; proof by contradiction.
         
      5.1 natural numbers; monoids; commutativity; semirings; cancellation; inverses; integers; rationals; rings; fields.
      5.2 unique existence.
      5.3 division theorem and algorithm.
         
      6.1 modular arithmetic.
      6.2 sets; membership; comprehension.
      6.3 sets of common divisors.
         
      7.1 gcd; Euclid's Algorithm.
      7.2 properties of gcds; Euclid's Theorem; fields of modular arithmetic.
         
      8.1 extended Euclid's Algorithm; integer linear combinations.
      8.2 Diffie-Hellman cryptographic method: shared secret key, key exchange.
         
      9.1 mathematical induction;
      9.2 Fundamental Theorem of Arithmetic.
      9.3 Euclid's infinitude of primes.
         
      10.1 sets; extensionality; subsets and supersets.
      10.2 separation principle; Russell's paradox; empty set; cardinality.
         
      11.1 powerset axiom; cardinality of powersets;
      11.2 powerset Boolean algebra.
         
      12.1 pairing axiom; ordered pairs; products.
      12.2 big unions; big intersections.
      12.3 union axiom; disjoint unions.
    Lent term
      13.1 relations; internal diagrams; relational extensionality.
      13.2 relational composition.
      13.3 relations and matrices.
         
      14.1 directed graphs; adjacency matrix.
      14.2 preorders; reflexive-transitive closure.
         
      15.1 partial functions.
      15.2 functions.
         
      16.1 retractions; sections; bijections; equal cardinality.
      16.2 equivalence relations; set partitions.
         
      17.1 calculus of bijections; characteristic functions.
      17.2 finite cardinality; infinity axiom.
         
      18.1 surjections; enumerability.
      18.2 uncountable and unbounded cardinality.
      18.3 axiom of choice.
      18.4 injections.
         
      19.1 direct and inverse images.
      19.2 replacement axiom; set-indexed constructions.
      19.3 foundation axiom; well-founded relations and induction.
• A note on enumerability.
• Exercises
  Michaelmas term
    On proofs
    On numbers
    More on numbers
    On induction
  Lent term

Formal Languages and Automata

• Videos

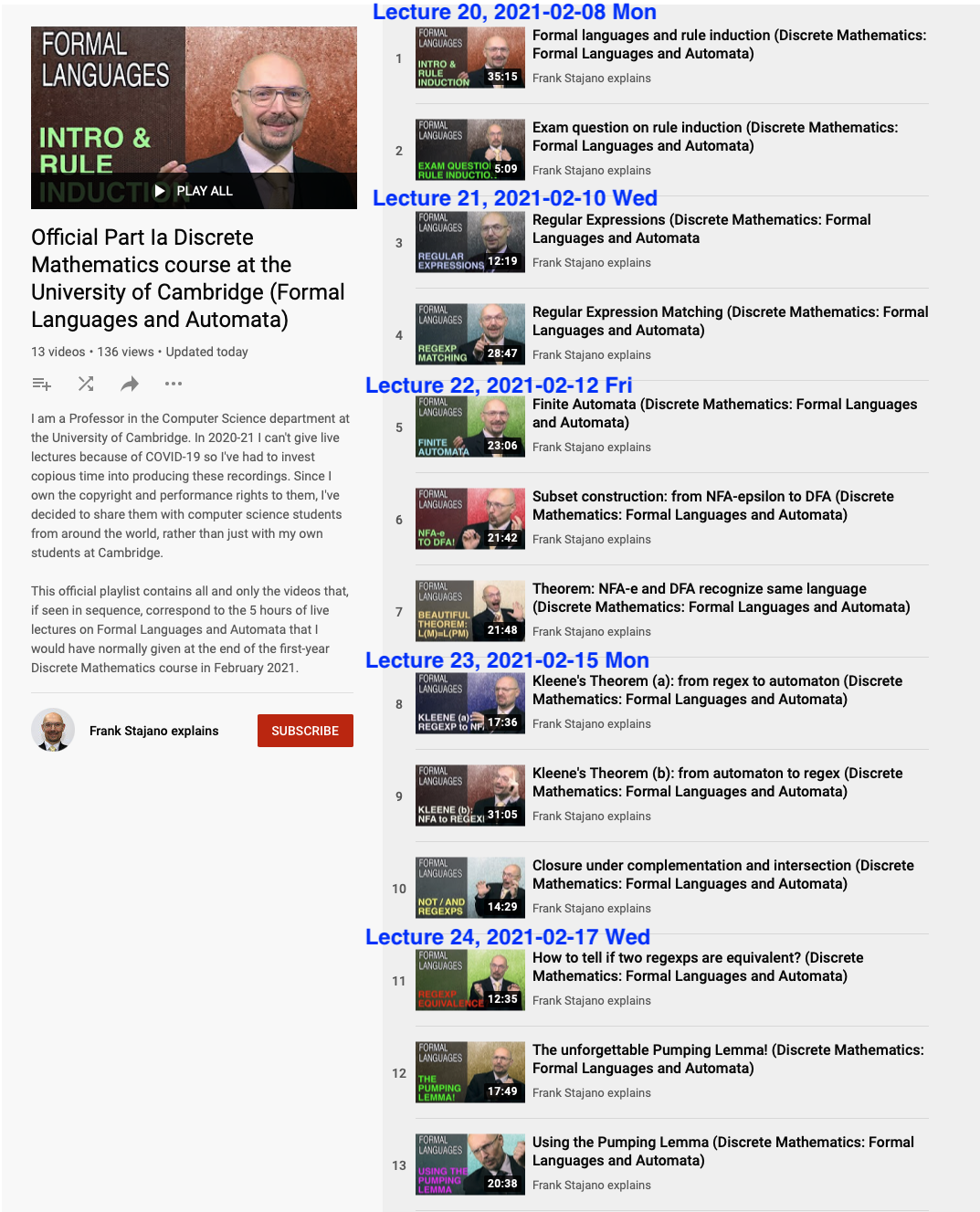
  The following annotated snapshot of the official playlist gives the mapping between the videos and the corresponding lectures. Taking advantage of the fact that we are not constrained by another class of students using the room and/or you having to run off to another lecture theatre, these virtual "lectures" are sometimes slightly shorter and sometimes slightly longer than 50 minutes, in order not to split an explanation in mid-topic. Subscribe to my channel, Frank Stajano Explains, to be notified whenever I publish new videos.

  

• Lecture notes (2 up, with large margins for your own scribbles)
• Lecture slides (1 up)
• Example sheet, including list of relevant past exam questions by topic