Course material 2010–11
Paid summer project. Did you enjoy this course? Did you take up the
programming microchallenges? Would you be interested in doing a paid
summer project this year under my supervision? If you are a brilliant
programmer and are also interested in
security, I want to
hear from you!
Passwords
are no longer acceptable as a security mechanism. I proposed a
clean-slate design to get rid of them: a portable gadget called Pico
that transforms your credentials from “what you know” into “what you
have”. To protect Pico against loss or theft, its storage is backed
up and encrypted and can only be unlocked by a key whose shares are
held by other devices worn by the user, the Picosiblings.
This project
will implement and prototype the backup and restore facility and the
interaction with the Picosiblings, including all the necessary
protocols for secret sharing, initial pairing etc. Development will
take place on Linux, with networked computers or VMs simulating the
various devices (Pico, docking station and Picosiblings). A port to
smartphone might be considered once the protocols have been debugged.
Algorithms II
2010–2011
Principal
lecturer: Dr Frank
Stajano
Email about this course sent by current students or
supervisors to name.surname--algs2 at cl.cam.ac.uk will be given
priority over that sent to other addresses.
Taken by: Part IB
Past exam questions can be found under Algorithms II but also, for historical reasons, under Data Structures and Algorithms (the parent course for both Algorithms I and Algorithms II); if you pick from the latter set, be sure to select questions dealing with topics covered in this year's syllabus.
Information for supervisors (contact lecturer for access, stating your name, CRSID and PhD supervisor)
Lecture handouts
Distributed during the first lecture on 2010-10-28. It will be to your advantage to bring your handout to every lecture, together with a notebook with non-detachable pages and a few coloured pens. Further printed copies of the handout are available from the student administration office. An electronic copy is also available: please do not print it again yourself and please do not circulate it outside cam.ac.uk.
Errata corrige
If you find any errors in the handout, please email me (at the --algs2 address mentioned above in order to get higher priority) and I'll credit you here and in the next edition.
| Page | Line | Errata | Corrige | Found on | by |
|---|---|---|---|---|---|
| 1 | -4 | stajano+algs2 | stajano--algs2 | 2010-10-18 | author |
| 16 | -2 | [delete footnote 13] | 2010-11-01 | author | |
| 18 to 20 | [Not really errors but I added various postconditions throughout and fixed inconsistent capitalizations.] | 2011-04-07 | author | ||
| 20 | 12 | with the smallest possible key (conceptually minus infinity) | with the largest possible delta (conceptually decreasing the key to minus infinity) | 2011-04-07 | author |
| 21 | -17 to -15 | Since the outcome of the linking step is that no two trees have the same degree, the number of trees is necessarily bounded by the highest degree (call it d) among those of the existing trees. Since c ≤ d, | For a given heap in a given state, call d the highest degree of any node in that heap; then, since the outcome of the linking step is that no two trees have the same degree, the number of trees is necessarily bounded by d + 1 (the case in which we have the trees of all possible degrees from 0 to d). Since c ≤ d by definition of d, | 2011-04-07 | Manfredas Zabarauskas |
| 22 | 6 to 8 | we must pay one coin for cutting and splicing it and another that must be stored in the new tree root, at a total cost of two coins (a constant). Therefore | we must pay a constant cost for cutting and splicing it and then we must store a gold coin in the new tree root; furthermore, if the parent of n was unmarked and was not a root, we must mark it and store two coins in it, at a total worst-case cost of four coins (one stored in the new root, two in the newly-marked node, and one coin's worth to cover all the actual work of cutting, splicing and marking). This is still a constant, therefore | 2010-11-04 | author |
| 33 | 22 to 23 | If el ∉ T, then T must have some other edge ex going across the cut, otherwise T wouldn't span the whole of G. | If el ∉ T, then adding it to T introduces a loop. For topological reasons, this loop must contain at least one other edge going across the cut and distinct from el: call any one of them ex. | 2011-01-21 | Myra VanInwegen |
| 45 | -14 | nodes of the pair on top | nodes of the pair through the edge(s) that directly join them, if any, on top | 2010-11-24 | author |
| 47 | 3 | bounded by the number of edges in the graph, |E|. | bounded by the length in edges of the longest path without cycles, |V| - 1. On the other hand, finding such a path, if it exists, for example with Breadth First Search or Depth First Search, will cost up to O(V + E). Each iteration thus costs O(E). | 2010-11-24 | author |
Timetable
Every Tuesday and Thursday at 1100 in LT1, starting Thu 2010-10-28 and ending Tue 2010-11-30 (10 lectures).
Student Feedback
In order to understand whether the lectures matched the expectations and hopes of the audience, I collected student feedback halfway through the course using this form. 34 students were kind enough to return a completed questionnaire. I find it more useful to collect feedback while the course is still running, rather than just at the end, so as to give current students a chance to benefit from any improvements that might result from their comments. At the end of the course I then collected student feedback again, receiving 27 responses. Thanks to all who participated and especially to the élite who programmed the algorithms as we went along.
Additional resources for individual lectures
If you want to own the material in this course, there is no better way than to implement it yourself in the programming language you most enjoy. I encourage you to do so.
Binomial heaps
Implement a binomial heap class with methods for (at least) merge, insert and extractMin. For I/O it's OK to render a binomial heap as a textual list, according for example to the following syntax:
tree = "[" root zero-or-more-trees "]". zero-or-more-trees = "" | tree | tree zero-or-more-trees. heap = "[" zero-or-more-trees "]".
Purely for extra enjoyment (but this skill will be useful for many other things we'll do in this course), once you've done the core programming you may find it fun to use the DOT language and the Graphviz toolkit to visualize the output of your program, as I did for the example I showed during the lecture.
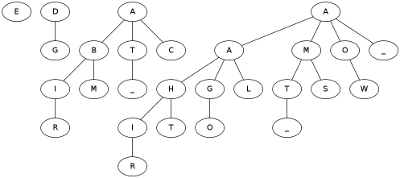
As test data to validate your implementation here is, in several formats, the binomial heap obtained after inserting into an empty one the characters of the string "ALGORITHMS_TWO_AT_CAMBRIDGE", in that order.
As a textual list:
[[E], [D, [G]], [A, [B, [I, [R]], [M]], [T, [_]], [C]], [A, [A, [H, [I, [R]], [T]], [G, [O]], [L]], [M, [T, [_]], [S]], [O, [W]], [_]]]
As a DOT graph.
As a picture obtained by processing the above .dot source with graphviz (click on the picture below to get the full animation I used in lectures):
The original paper on binomial heaps is available from the ACM digital library (or cached).
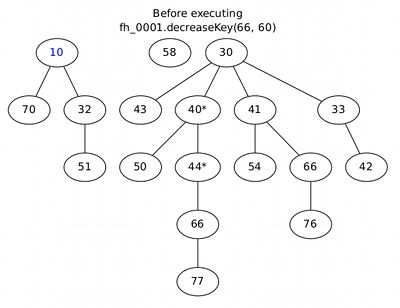
Fibonacci heaps
Implement a circular-doubly-linked-list class with methods for (at least) insert, merge and extractMin. As usual, for I/O it's ok to just render the list as text: what matters is to do all the internal pointer juggling properly.
If you think you're a good programmer, unit-test your code too: initially boring perhaps, but very rewarding later.
If you think you're a great programmer, implement a full Fibonacci heap class, including extractMin and decreaseKey. Do whatever you like for I/O. A good recommendation while you're just writing and unit-testing the core code is a textual list, as above, but it can get a little hard to read. For a reference during debugging you may wish to compare your results against this fancier graphical output (the picture links to the pdf I used in lectures, which has a full execution trace):
The original paper on Fibonacci heaps is available from the ACM digital library (or cached).
Dr Alastair Beresford points out this interesting discussion about the performance of Fibonacci heaps.
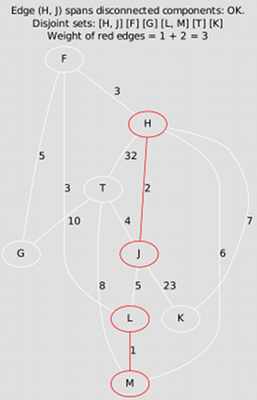
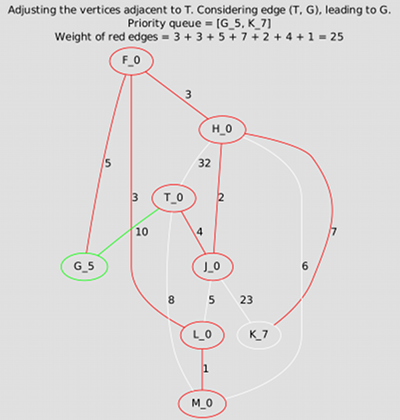
Minimum Spanning Tree
Write programs to compute the minimum spanning tree of a given connected, weighted, undirected graph using the algorithms of Kruskal and Prim. The programs that produce the animations shown below were implemented using Vertex and Edge objects and adjacency lists; but, leaving visualization aside for the moment, the quickest approach may instead be to use the adjacency matrix. Do whatever you prefer, then compare your results with the ones below. For more examples, see your textbook.
With Kruskal, the subset of the MST may initially be a forest:
With Prim, instead, it remains a tree throughout:
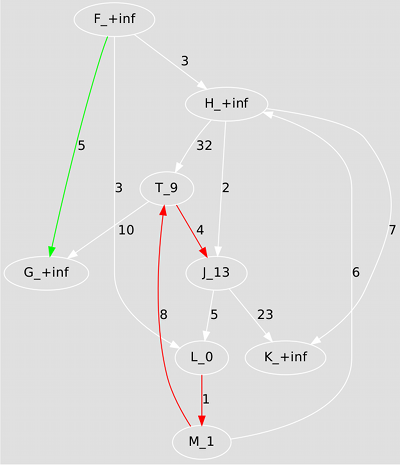
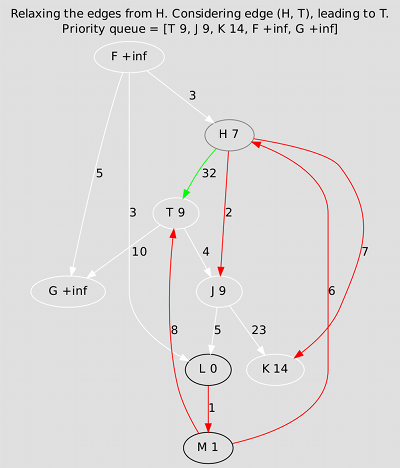
Single Source Shortest Paths
Write programs to compute the shortest paths from a designated source node to all the other nodes of a directed, weighted graph, using the algorithms of Bellman-Ford and Dijkstra. Again, using the adjacency matrix and not bothering with visualization will be much quicker. First reproduce the results below, then try feeding your programs a graph with negative edge weights, then one with negative weight cycles, and check whether they behave as you expect them to. (Ideally you'd also make up your mind about exactly what to expect before writing the programs!)
Bellman-Ford is somewhat over-enthusiastic but tough and reliable:
Dijkstra is more subtle and more efficient, but can't always be used:
Maximum flow
Write a program that, given the .dot source for a flow network, spits out the .dot source for its residual network. The boring and not-relevant-for-this-course part of this job is parsing the .dot input file; if you want to skip that, operate on an adjacency matrix representation and optionally write out the .dot representation for both the input and the output, just so as to be able to check visually whether everything is as expected.
Computational geometry
Challenge: can you write a program to do Jarvis's march in one pass, without splitting the process into an upwards pass on the right and a distinct downwards pass on the left? And still using only the cross product rather than computing angles? Is it really impossible?
$Id: index-b.html 41 2011-05-05 12:52:41Z fms27 $