Advanced Graphics

Examples class 2

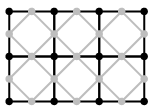• The Doo-Sabin subdivision scheme is illustrated in the "Part A" study guide in Figure 13. The Reif-Peters scheme is illustrated in the diagram on the right. Reif-Peters uses a different approach to Doo-Sabin: in it the new points are generated halfway between existing points and connected up into a mesh as illustrated in the diagram on the right (black: original mesh; grey: new mesh). Note that (i) the existing points do not form part of the new mesh and (ii) each new point's position is simply the average of the positions of the two existing points at either end of the corresponding line segment.
  • Doing the Reif-Peters subdivision twice produces a mesh which looks similar to that produced by doing the Doo-Sabin subdivision once (Figure 13 (left)). You can treat two steps of Reif-Peters as if it were a single step of a Doo-Sabin-like subdivision scheme. Calculate the weights on the original points for each new point after two steps of Reif-Peters (i.e. work out what numbers replace those in Figure 13 (right) for the Reif-Peters two step scheme). [2 marks]
  • For the Reif-Peters one step scheme, explain what happens around extraordinary vertices and what happens around extraordinary polygons, giving examples. [2 marks]
• [2003 P7 Q4 (c)] The Catmull-Clark bivariate subdivision scheme is a bivariate generalisation of the univariate 1/8 [1, 4, 6, 4, 1] subdivision scheme. It creates new vertices as blends of old vertices in the following ways:
  
  
  • Provide similar diagrams for the bivariate generalisation of the univariate four-point interpolating subdivision scheme 1/16 [-1, 0, 9, 16, 9, 0, -1]. [5 marks]
  • Explain what problems arise around extraordinary vertices (vertices of valency other than four) for this bivariate interpolating scheme and suggest a possible way of handling the creation of new edge vertices when the old vertex at one end of the edge has a valency other than four. [4 marks]
• [2004 P7 Q4 (c)] The Loop and Butterfly subdivision schemes can both operate on triangular meshes, in which all of the polygons have three sides. Both schemes subdivide the mesh by introducing new vertices at the midpoints of edges, splitting every original triangle into four smaller triangles, as shown below.
  
  
  Each scheme has rules for calculating the locations of the new "edge" and "vertex" vertices based on the locations of the old vertices. These rules are shown above. All weights should be multiplied by 1/16.
  • Which of the two schemes produces a limit surface which interpolates the original data points?
  • Which of the four rules must be modified when there is an extraordinary vertex? For each of the four rules either explain why it must be modified or explain why it does not need to be modified.
  • Suggest appropriate modifications where necessary to accommodate extraordinary vertices.
  [9 marks]
• [2008 P9 Q7 (c)] State and explain the radiosity equation. [4 marks]
• [1999 P9 Q4] Outline an efficient method used to calculate view factors for radiosity. [4 marks]
• What is photon mapping used for? [2 marks]
  Describe Monte Carlo integration, and explain where it is used within photon mapping. [4 marks]
• [2004 P9 Q6 (b)] Explain how a plane can be used as a Computational Solid Geometry (CSG) primitive. [2 marks]
• [2004 P9 Q6 (c)] List the three binary operations used in CSG. Explain how a CSG object can be represented as a binary tree. Describe an algorithm to find the first intersection point between a ray and an arbitrary CSG object. Assume that there are already algorithms which you can use to find the intersection points between the ray and each type of CSG primitive. Ensure that you state any assumptions you make about the information provided to you by these ray-primitive intersection algorithms. [8 marks]
• [2003 P9 Q6 (c)] Show how the following object can be constructed using Constructive Solid Geometry (CSG). You may assume the following primitives: sphere, cylinder, cone, torus, box. [You are expected to describe which primitives are needed and how they are combined but you are not expected to specify accurately all of the parameters of the primitives.] [4 marks]
  
  

This exercise set is marked out of 50. This should take 90 minutes in an examination.