Course pages 2013–14
Experimental Methods
An introduction to data analysis using Excel
Many simple statistical analyses can be performed using Microsoft Excel.
Preliminaries
For some statistical tests in Excel, it is necessary to load the Analysis ToolPak:
- Office button - Excel Options - Add-Ins - Go...
- Select Analysis ToolPak and click OK (may need to install)
Examples of different techniques will be illustrated with some data from Chapter 4 of Lazar (Table 4.11). It could be entered in Excel as follows:
| A | B | C | D | |
|---|---|---|---|---|
| 1 | Lazar et al | |||
| 2 | Table 4.11 | |||
| 3 | ||||
| 4 | Participant | Standard | Prediction | Speech |
| 5 | 1 | 245 | 246 | 178 |
| 6 | 2 | 236 | 213 | 289 |
| 7 | 3 | 321 | 265 | 222 |
| 8 | 4 | 212 | 189 | 189 |
| 9 | 5 | 267 | 201 | 245 |
| 10 | 6 | 334 | 197 | 311 |
| 11 | 7 | 287 | 289 | 267 |
| 12 | 8 | 259 | 224 | 197 |
| 13 | Mean | |||
| 14 | SD |
Warning: The same set of data will be analysed here as if it has been collected in several different ways. Any real data could only be analysed in ways that were appropriate for the design of the experiment.
Visual inspection
Inspect the data by grouping it into bins and plotting the resulting histogram.
Augment the previously entered data with a set of bins sizes by typing 175 into cell f5, 200 into f6 and so on up to 350 in f12. Then:
- Go to the Data tab and click on Data Analysis
- Select Histogram and click OK
- Select Input Range: (b5:b12 for this example)
- Select Bin Range: (f5:f12 for this example)
If you omit this, Excel will choose defaults that span the range of values. - Select Output Range: (the top left cell: h4 for this example)
- Tick Chart Output
- Click OK
The charts are easier to read if the heading and legend are removed.
Repeat this for the Prediction and Speech timings (putting the results at h15 and h16 for this example). Note that there are no values in any of the charts below the bottom bin value of 175 or above the top value of 350.
Superimpose normal distribution
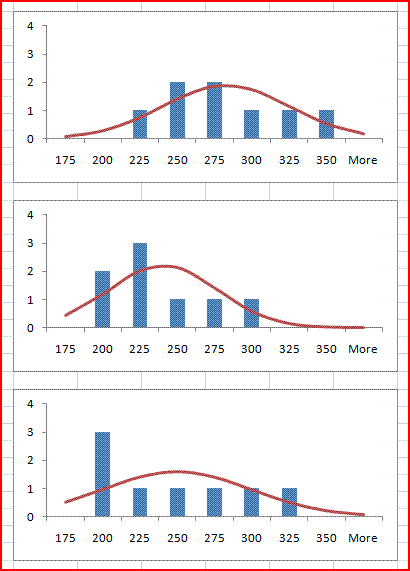
Most of the statistical tests rely on the underlying population data having a normal distribution. This can be checked visually by superimposing a normal distribution curve over the histogram.
Calculate the mean and standard deviation of each data series using the built-in Excel functions:
- AVERAGE(range)
- STDEV(range)
putting the results in b13:d14.
Calculate the bin values for a normal distribution with the same mean, standard deviation and number of samples using:
- NORMDIST(value,mean,sd,TRUE)
putting the results in r5:r12. It is also necessary to invent extra values at either end of the range in r4 and r13. Calculate the differences multiplied by the number of samples in s5:s13.
Add these as a line on the chart:
- Right click on a histogram bar and select Select Data...
- Click Add
- Give the series a name like Normal, select the values just calculated and click OK twice to give a second set of histogram bars.
- Right click on one of the new bars and select Change Series Chart Type...
- Select Line and click OK.
- Right click on the line and select Format Data Series...
- Under Line Style tick Smoothed line and click Close
Repeat this for the other two measures. Excel scales the data to fill the chart space, but it would be better if the three graphs had the same ranges on their axes to allow comparison. Select the vertical axis in the first chart, right click and use Format Axis... to fix the maximum value at 4.
There are not really sufficient samples to be definite, but it seems plausible to treat the underlying distributions as normal.
Investigating relationships
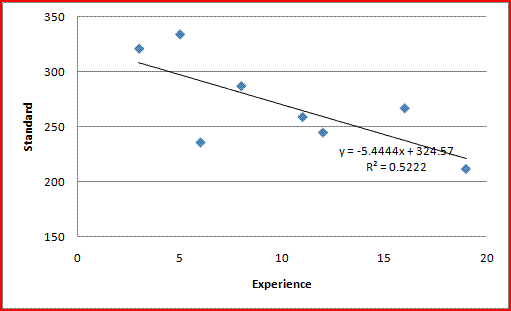
Each participant's number of years' experience using computers can be copied from Lazar Table 4.20, and then the correlation with the standard data entry time investigated as follows:
- Enter the data (12,6,3,19,16,5,8,11) in cells a5:a12 and change the heading in a4 to Experience
- Select a4:b12
- Go to the Insert tab and click on Scatter with only markers
- Right click on the y axis and select Format Axis...
- Fix the minimum value at something like 150 and the maximum at something like 350
- Right click on a data point and select Add Trendline...
- Tick the Display Equation and Display R-squared boxes
Observe that the slope of the least-squares line is negative, and that the squared Pearson correlation coefficient R2 is 0.5222.
Box plots
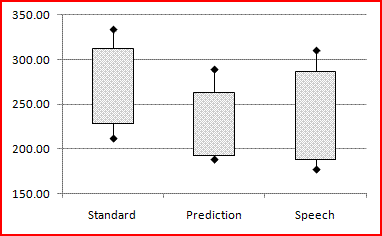
The distributions can be compared using box plots:
- For each of the three data series, calculate the mean minus the standard deviation, the maximum value, the minimum value, and the mean plus the standard deviation, putting the results in b17:d20.
- Replicate the headings from b4:d4 in b16:d16.
- Select the table including the row and column headings, and insert an Open-High-Low-Close stock chart selecting the Switch Row/Column option.
- Move and resize the chart somewhere convenient, say in a22:f35, and remove the legend from the right.
- The high-low lines are clearer with diamond end points.
A box covering the range from mean-sd to mean+sd will show approximately the 15th and 85th percentiles. Use mean±2sd/3 for an approximation to quartiles.
Z-value transformation
It is often convenient to normalise data by subtracting its mean and dividing by its standard deviation to give a Z-value. Excel has a built-in function for this:
- STANDARDIZE(value,mean,sd)
The standardized values should have a mean of 0 and a standard deviation of 1.
t test
The graphs and box plots suggest that the task completion time for predictive entry is less than for standard entry. This can be checked with a t test:
- Go to the Data tab and click on Data Analysis
- Select t-Test: Two-Sample Assuming Unequal Variances and click OK
- Select Variable 1 Range: (b4:b12 for this example)
- Select Variable 2 Range: (c4:c12 for this example)
- Select Labels in First Row
- Select Output Range: (the top left cell: h36 is convenient for this example)
- Click OK
Observe that t Stat is 2.16878 and P(T<=t) one-tail is 0.023906. This would be reported as:
An independent-samples t test showed a significant effect of the predictive software against the standard input on the task completion time (t(14) = 2.17, p < 0.05).
If the data had been collected in a paired-samples experiment, the analysis would use t-Test: Paired Two Sample for Means. In this case, t Stat is 2.631264 and P(T<=t) one tail is 0.016925. This would be reported as:
A paired-samples t test showed a significant effect of the predictive software against the standard input on the task completion time (t(7) = 2.6, p < 0.05).
The graphs also suggest that there is little difference between predictive and speech-based entry. A t test shows that t Stat is -0.43246 and P(T<=t) one-tail is 0.33625. This would be reported as:
An independent-samples t test showed no significant difference between the speech and predictive software on the task completion time (t(13) = 0.432, p > 0.05).
One-way ANOVA
Analysis of variance compares the means of two or more groups. (If there are only two groups, this is the same as a t test.)
- Data - Data Analysis
- Select Anova: Single factor and click OK
- Select Input Range: (b4:d12 for this example)
- Select Grouped by Columns
- Select Labels in First Row
- Select Output Range: (the top left cell: h51 is convenient for this example)
- Click OK
Observe that F is 2.173781 and P-value is 0.138667. This would be reported as:
A one-way ANOVA test showed no significant effect of the three input methods on the task completion time (F(2,21) = 2.17, p > 0.05).
