Computer Laboratory – Course material 2008–09: Digital Signal Processing

Next: Natural Language Processing Up: Lent Term 2009: Part Previous: Computer Vision Contents

Digital Signal Processing

Lecturer: Dr M.G. Kuhn

No. of lectures: 12

Prerequisite courses: Probability, Mathematical Methods for Computer Science
The last lecture of Unix Tools (MATLAB introduction) is a prerequisite for the practical exercises. Some of the material covered in Information Theory and Coding and Floating-Point Computation will also help in this course.

Aims

This course teaches the basic signal-processing principles necessary to understand many modern high-tech systems, with a particular view on audio-visual data compression techniques. Students will gain practical experience from numerical experiments in MATLAB-based programming assignments.

Lectures

Signals and systems. Discrete sequences and systems, their types and properties. Linear time-invariant systems, convolution.
Phasors. Eigen functions of linear time-invariant systems. Review of complex arithmetic. Some examples from electronics, optics and acoustics.
Fourier transform. Phasors as orthogonal base functions. Forms of the Fourier transform. Convolution theorem, Dirac's delta function, impulse combs in the time and frequency domain.
Discrete sequences and spectra. Periodic sampling of continuous signals, periodic signals, aliasing, sampling and reconstruction of low-pass and band-pass signals, spectral inversion.
Discrete Fourier transform. Continuous versus discrete Fourier transform, symmetry, linearity, review of the FFT, real-valued FFT.
Spectral estimation. Leakage and scalloping phenomena, windowing, zero padding.
Finite and infinite impulse-response filters. Properties of filters, implementation forms, window-based FIR design, use of frequency-inversion to obtain high-pass filters, use of modulation to obtain band-pass filters, FFT-based convolution, polynomial representation, z-transform, zeros and poles, use of analog IIR design techniques (Butterworth, Chebyshev I/II, elliptic filters).
Random sequences and noise. Random variables, stationary processes, autocorrelation, crosscorrelation, deterministic crosscorrelation sequences, filtered random sequences, white noise, exponential averaging.
Correlation coding. Random vectors, dependence versus correlation, covariance, decorrelation, matrix diagonalization, eigen decomposition, Karhunen-Loève transform, principal component analysis. Relation to orthogonal transform coding using fixed basis vectors, such as DCT.
Lossy versus lossless compression. What information is discarded by human senses and can be eliminated by encoders? Perceptual scales, masking, spatial resolution, colour coordinates, some demonstration experiments.
Quantization, image and audio coding standards. A/ 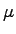$\mu$ -law coding, delta coding, JPEG photographic still-image compression.
MPEG standards. Motion compensation, video coding, MP3.

Objectives

By the end of the course students should

be able to apply basic properties of time-invariant linear systems
understand sampling, aliasing, convolution, filtering, the pitfalls of spectral estimation
be able to explain the above in time and frequency domain representations
be competent to use filter-design software
be able to visualize and discuss digital filters in the z-domain
be able to use the FFT for convolution, deconvolution, filtering
be able to implement, apply and evaluate simple DSP applications in MATLAB
apply transforms that reduce correlation between several signal sources
understand and explain limits in human perception that are exploited by lossy compression techniques
provide a good overview of the principles and characteristics of several widely-used compression techniques and standards for audio-visual signals

Recommended reading

* Lyons, R.G. (2004). Understanding digital signal processing. Prentice Hall (2nd ed.).
Oppenheim, A.V. & Schafer R.W. (1999). Discrete-time digital signal processing. Prentice Hall (2nd ed.).
Stein, J. (2000). Digital signal processing - a computer science perspective. Wiley.
Salomon, D. (2002). A guide to data compression methods. Springer.

Next: Natural Language Processing Up: Lent Term 2009: Part Previous: Computer Vision Contents