The MetiTarski Theorem Prover
MetiTarski is an automatic theorem prover based on a combination of resolution and a decision procedure for the theory of real closed fields. It is designed to prove theorems involving real-valued special functions such as log, exp, sin, cos and sqrt. In particular, it is designed to prove universally quantified inequalities involving such functions. This problem is undecidable, so MetiTarski is necessarily incomplete. Nevertheless, MetiTarski is remarkably powerful. Here are a few of the hundreds of theorems that it can prove, automatically and in seconds.
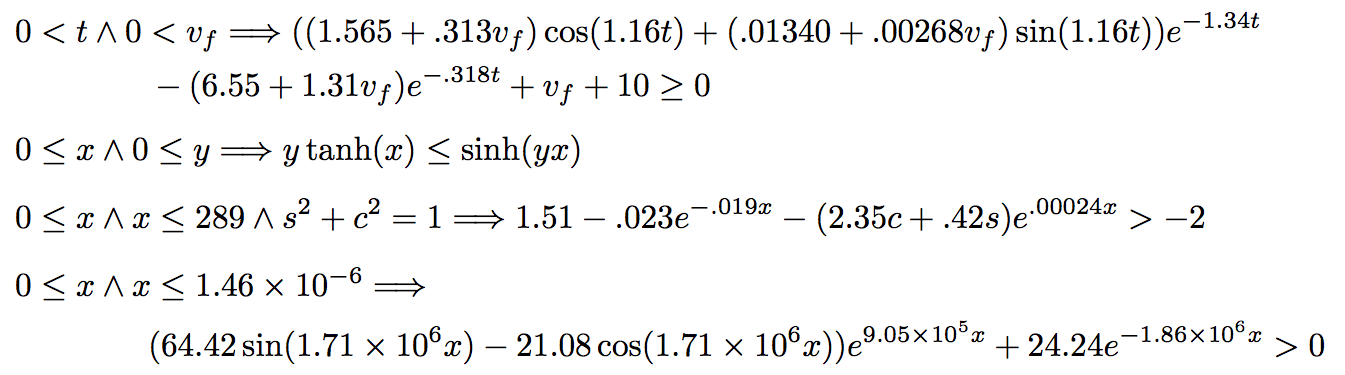
MetiTarski (version 2.4, released 21 October 2014) is available to download.![]()
MetiTarski is described in the following papers:
- Behzad Akbarpour and L. C. Paulson.
Towards automatic proofs of inequalities involving elementary functions. In: Byron Cook and Roberto Sebastiani (editors), PDPAR 2006: Pragmatics of Decision Procedures in Automated Reasoning, 27–37. - Behzad Akbarpour and Lawrence C. Paulson.
Extending a resolution prover for inequalities on elementary functions. In: Nachum Dershowitz and Andrei Voronkov (editors), Logic for Programming, Artificial Intelligence, and Reasoning — LPAR 2007 (Springer LNCS 4790), 47–61. Publisher's version - Behzad Akbarpour and L. C. Paulson.
MetiTarski: An automatic prover for the elementary functions. In: Serge Autexier et al. (editors), Intelligent Computer Mathematics (Springer LNCS 5144, 2008), 217–231. (Proceedings of Calculemus 2008.) Publisher's version. Slides available. - Behzad Akbarpour and L. C. Paulson.
Applications of MetiTarski in the verification of control and hybrid systems. In: Rupak Majumdar and Paulo Tabuada (editors), Hybrid Systems: Computation and Control (Springer LNCS 5469, 2009), 1–15. Publisher's version - Behzad Akbarpour and L. C. Paulson.
MetiTarski: An automatic theorem prover for real-valued special functions. J. Automated Reasoning 44 3 (2010), 175–205. Publisher's version - William Denman, Behzad Akbarpour, Sofiène Tahar, Mohamed H. Zaki and L. C. Paulson.
Formal verification of analog designs using MetiTarski.
In: Armin Biere and Carl Pixley (editors), Formal Methods in Computer Aided Design (2009), 93–100. Publisher's version - Rajeev Narayanan, Behzad Akbarpour, Mohamed H. Zaki, Sofiène Tahar and L. C. Paulson.
Formal verification of analog circuits in the presence of noise and process variation. In: DATE 2010: Design, Automation and Test in Europe, 1309–1312. - James P. Bridge and Lawrence C. Paulson.
Case Splitting in an automatic theorem prover for real-valued special functions.
J. Automated Reasoning 50 1 (2013), 99–117. Raw data available • Publisher's version at www.springerlink.com - Grant O. Passmore, Lawrence C. Paulson and Leonardo de Moura.
Real algebraic strategies for MetiTarski proofs. In: Johan Jeuring (editor), Conferences on Intelligent Computer Mathematics --- CICM 2012 (Springer LNCS 7362, 2012), 358–370. Publisher's version at www.springerlink.com - MetiTarski: past and future.
Interactive Theorem Proving --- ITP 2012
Princeton, New Jersey, August 2012.
Publisher's version at www.springerlink.com • Slides available - MetiTarski's Menagerie of Cooperating Systems.
Keynote Lecture for the FroCoS and Tableaux conferences.
Nancy, France, September 2013.
Publisher's version at www.springerlink.com • Slides available - Automated theorem proving for special functions: the next phase.
Keynote Lecture for SNC 2014 (Symbolic-Numeric Computation).
Shanghai, China, July 2014.
Slides available - Samuel Coward, L. C. Paulson, Theo Drane and Emiliano Morini.
Formal verification of transcendental fixed and floating point algorithms using an automatic theorem prover.
Formal Aspects of Computing 34:2 (2022), 1–22
Research supported by the Engineering and Physical Sciences Research Council [grant numbers EP/C013409/1 and EP/I011005/1]. MetiTarski is a modified version of Joe Hurd's Metis prover.