Introduction to Functional Programming
2002-03

Exercise Sheets

NOTE: You are now in a position to do all three sheets!

1. Sheet one
2. Sheet two
3. Sheet three

Lectures

Lecture 1: Thursday 15th January

Material covered: Slides 1-12

This was a general introduction lecture to motivate the course. (Not helped by the projector not working. Funnily it started working at 11:03!)

I strongly recommend that you download an SML implementation and play. There are a number of good ones:

• SML/NJ. I use this one in the lectures.
• Moscow ML. Another great implementation.
• MLj. A compiler from SML to Java bytecodes. Includes Java interop!
• SML.NET. A .NET SML compiler from Microsoft Research. Includes VS support!
• OCAML. Probably the best ML compiler out there, but uses a French dialect (not SML) and includes lots of fancy features.

A paper detailing the prototyping experiment that I mentioned at the end of today's lecture can be found here (ps).

Lecture 2: Tuesday 20th January

Material covered: Slides 13-25

Finally we got our hands on an SML implementation, and we did some elementary coding. We saw integers, reals, characters and strings. We also saw the wonder of n-ary tuples.

You can read about the SML basis library here

Lecture 3: Thursday 22nd January

Material covered: Slides 26-33

Today we did some cool programming with lists. We saw the beautifully concise ML code to append and reverse lists. We also noticed that our length and reverse functions weren't that efficient, but we were able to code up efficient versions (and they're still beautiful!).

Lecture 4: Tuesday 27th January

Material covered: Slides 34-41

Today we started off with a quick revision of what iterative functions were in ML. We then got on to looking at two sorting algorithms:

1. Insertion sort This was dead easy to understand, but we had to wait a long time to see it sort 10,000 reals
2. Quicksort The king of algorithms. Even cooler is that it's so beautifully clear in ML! We also saw it sort 10,000 reals in around 160msecs!!!

Lecture 5: Thursday 29th January

Material covered: Slides 42-51

Today we started with ML records. We then got on to the wonderful world of recursive datatype declarations. Isn't ML powerful? It's so easy to define complicated datatypes, and then pattern matching makes processing them really neat. depth and preorder etc. were particularly compact and readable.

Homework: Slide 50 contains code for three different ways of list tree elements. They're nice but use appends. Can you code them more efficiently?

Lecture 6: Tuesday 3rd February

Material covered: Slides 52-58

Today we did two funky things with trees, we simulated

1. Arrays (although it's not as efficient as we might like); and
2. Dictionaries (nice search time)

We also looked at the sum datatype, which has two type variables! Some code is available here

Lecture 7: Thursday 5th February

Material covered: Slides 59-68

Today we entered the wonderful world of higher-order functions. ML allows you to pass in functions as arguments to other functions, and even allows functions to return a function as the result. Wow! We saw some neat matrix multiplication using these ideas. We also saw some "design patterns": the map, foldl and foldr functionals.

Oops! I forgot to clarify one important point. We saw that ML allowed us to write curried functions, e.g. instead of

fun sum (m,n) = m+n

of type int*int -> int we could write

fun sum m = fn n => m+n;

of type int -> (int -> int). ML provides a nice shorthand for the above code:

fun sum m n = m+n;

i.e. the space between the arguments means that the code is curried! This function is of type int -> (int -> int)

Lecture 8: Tuesday 10th February

Material covered: Slides 69-77

Today we observed the lecturer's laptop decide that it was too old to be bothered to talk with projectors :-( We looked at how we can define lazy lists, i.e. lists where the next element is evaluated on demand. This allowed us to define sequences that were infinite!

Here is some code that generates an infinite tree of strings built up from characters A, B, and C, and selects those strings that are palindromes by both breadth-first and depth-first walking over the tree.

Lecture 9: Thursday 12th February

Material covered: Slides 78-86

Today we looked at proving some properties of ML code. Having proved that the code satisfies the property we don't need to bother with testing!

Lecture 10: Tuesday 17th February

Material covered: Slides 87-95

Today we continued our study of proving properties of ML code. We looked at structural induction, and we proved some properties of code that worked on lists and on trees.

We also saw the coolest demos of FRAN - Conal Elliot's declarative approach to animation.

We went wow! at things like this:

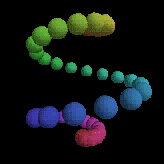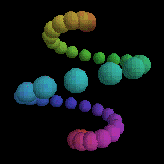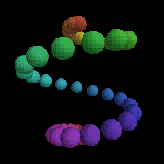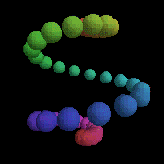
which is generated from the following five lines of Haskell:

spiralTurn = turn3 zVector3 (pi*time) (unionGs (map ball [1 .. n])) where n = 40 ball i = withColorG color ( move3 motion ( stretch3 0.1 sphereLowRes )) where motion = vector3Spherical 1.5 (10*phi) phi phi = pi * fromInt i / fromInt n color = colorHSL (2*phi) 0.5 0.5

Lecture 11: Thursday 19th February

Material covered: Slides 96-109

Today we looked in more detail at SML's type system. In particular we looked quite carefully at how ML infers a type for an expression.

NOTE: The best way to understand this is to attempt some examples yourself. Try to work out the types of the following functions:

• fn x => fn f => f(f(x))
• fn f => fn g => fn x => f(g(x))
• fn f => fn g => fn x => f x (g x)
• map
• foldr
• foldl

Lecture 12: Tuesday 24th February

Material covered: Slides 110-end

Today we looked at a cute application area for SML: writing parsers. We discovered that the code for a parser looks almost exactly like the grammar: Cool!

Errata

• Slide 33. (Unfortunate) Here I give my own definition of the take and drop functions. Unfortunately they take their arguments in the opposite order to the inbuilt List.take and List.drop functions. Not an error, but potentially misleading!