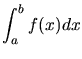

Next: Differential Equations and Computational
Up: No Title
Previous: Taylor Series
The most fundamental notion in continuous mathematics is the
idea of a limit: the value that an expression
inexorably approaches, possibly from below, possibly from above,
possibly oscillating around it, tending always closer but
possibly never actually reaching it. We have already encountered limits in
the power series definitions of transcendental functions. When computers
try to calculate something as seemingly straightforward as
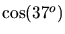 , they
merely approximate it by truncating (considering a finite number of terms
in) an infinite series whose limit is
, they
merely approximate it by truncating (considering a finite number of terms
in) an infinite series whose limit is
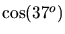 . The entire
monumental edifice of The Calculus - invented in the decades
before 1700 independently
by Isaac Newton and Gottfried Leibniz, described by John von Neumann as
``the first achievement of modern mathematics, and
the greatest technical advance in exact thinking" - is built upon the
notion of the limit.
. The entire
monumental edifice of The Calculus - invented in the decades
before 1700 independently
by Isaac Newton and Gottfried Leibniz, described by John von Neumann as
``the first achievement of modern mathematics, and
the greatest technical advance in exact thinking" - is built upon the
notion of the limit.
Here are some properties of limits, for continuous functions
f(x) and g(x):
![$\displaystyle \lim_{x \rightarrow c}[f(x)+g(x)]$](img42.gif) |
= |
![$\displaystyle \lim_{x \rightarrow c}[f(x)] +
\lim_{x \rightarrow c}[g(x)]$](img43.gif) |
(14) |
| |
|
|
|
![$\displaystyle \lim_{x \rightarrow c}[f(x)-g(x)]$](img44.gif) |
= |
![$\displaystyle \lim_{x \rightarrow c}[f(x)] -
\lim_{x \rightarrow c}[g(x)]$](img45.gif) |
(15) |
| |
|
|
|
![$\displaystyle \lim_{x \rightarrow c}[f(x)g(x)]$](img46.gif) |
= |
![$\displaystyle \lim_{x \rightarrow c}[f(x)]
\lim_{x \rightarrow c}[g(x)]$](img47.gif) |
(16) |
| |
|
|
|
![$\displaystyle \lim_{x \rightarrow c}[kf(x)]$](img48.gif) |
= |
![$\displaystyle k\lim_{x \rightarrow c}[f(x)]$](img49.gif) |
(17) |
| |
|
|
|
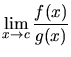 |
= |
![$\displaystyle \frac{\lim_{x \rightarrow c}
[f(x)]}{\lim_{x \rightarrow c}[g(x)]} \; \; {\rm assuming } \; \;
(\lim_{x \rightarrow c}[g(x)] \ne 0)$](img51.gif) |
(18) |
The basic concept of the derivative
of a function f(x), denoted f'(x) or
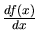 , signifying its instantaneous rate of change at
a point x,
is defined as the limit of its Newton Quotient at that point:
, signifying its instantaneous rate of change at
a point x,
is defined as the limit of its Newton Quotient at that point:
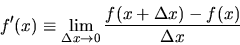 |
(19) |
The derivative of f(x) exists wherever the above limit exists. It will exist
near any point where
f(x) is continuous, i.e. if near any point c in the domain of
f(x), it is true that
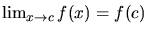 .
.
Review of Rules of Differentiation (material
not lectured)
- The derivatives of power functions obey a simple rule about exponents:
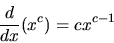 |
(20) |
- For any differentiable function f(x) and some constant c,
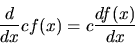 |
(21) |
- If u and v are differentiable functions of x, then their sum u+vis a differentiable function of x and
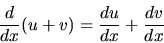 |
(22) |
- The product of two differentiable functions u and v is differentiable,
and
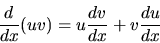 |
(23) |
- If u is some differentiable function of x and c is a constant,
then uc is differentiable, and
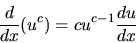 |
(24) |
- At any point where
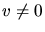 ,
the quotient u/v of two differentiable functions
u and v is itself differentiable, and its derivative is equal to:
,
the quotient u/v of two differentiable functions
u and v is itself differentiable, and its derivative is equal to:
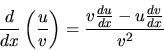 |
(25) |
- The Chain Rule:
if y is a differentiable function of u, and u is a
differentiable function of x, then y is a differentiable function of x,
and in particular:
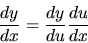 |
(26) |
In another form: if f(x) is differentiable at x, and g(f(x)) is
differentiable at f(x), then the composite 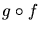 is
differentiable at x and
is
differentiable at x and
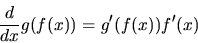 |
(27) |
For a continuous function f(x) that is sampled only at a set of discrete
points
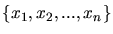 , an estimate of the derivative is
called the finite difference. It is defined as you might expect:
, an estimate of the derivative is
called the finite difference. It is defined as you might expect:
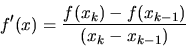 |
(28) |
When using a computer to calculate derivatives of continuous data or signals,
they must be sampled at a finite number of points; then the above finite
difference becomes an estimator of the instantaneous derivative.
Clearly, the finite difference approaches the instantaneous derivative
in the limit that the sampling interval becomes small:
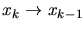 .
.
The area A under a function between two definite points is called its
definite integral, and it can be calculated in several ways.
Numerically, it can be estimated as the limit of a sum of small rectangular
areas inscribed under the function, each of whose height is equal to the
value of the function at that point, and whose width 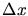 shrinks
to zero:
shrinks
to zero:
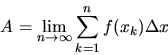 |
(29) |
Such a summation is the definite integral of the function over the domain
covered by the shrinking rectangles, and the origin of the integral sign
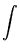 is the letter S in the Latin word Summa, for sum. Thus we denote
is the letter S in the Latin word Summa, for sum. Thus we denote
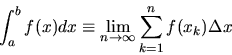 |
(30) |
where the set of samples f(xk) is taken uniformly
from x1=a to xn=b, and so
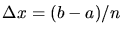 . The above expression
is also termed a Riemann Integral.
. The above expression
is also termed a Riemann Integral.
Many of the properties we noted earlier for limits obviously apply to
definite integrals, since they are themselves defined as limits. For example:
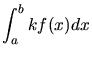 |
= |
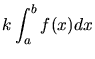 |
(31) |
| |
|
|
|
![$\displaystyle \int_{a}^{b} [ f(x) + g(x)] dx$](img75.gif) |
= |
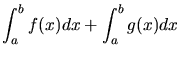 |
(32) |
| |
|
|
|
![$\displaystyle \int_{a}^{b} [ f(x) - g(x)] dx$](img77.gif) |
= |
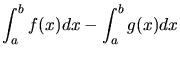 |
(33) |
| |
|
|
|
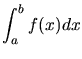 |
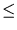 |
![$\displaystyle \int_{a}^{b} g(x) dx \; \; {\tt if} \; \; f(x) \le g(x)
\; \; {\tt on} \; \; [a,b]$](img81.gif) |
(34) |
| |
|
|
|
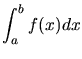 |
+ |
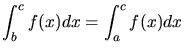 |
(35) |
The antiderivative of f(x) is denoted F(x) and it is the
function whose derivative is f(x), i.e. that function which satisfies
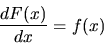 |
(36) |
Often one can find the antiderivative of f(x) simply by applying the
rules for differentiation in reverse. For example, since we know that
if n is a positive integer
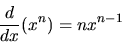 |
(37) |
we can infer that if
f(x) = xn, then its antiderivative is:
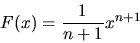 |
(38) |
Because these are relatively simple symbol-manipulating rules, they can
easily be programmed into symbolic math packages such as Stephen Wolfram's
famous Mathematica, and also Macsym, to generate the
antiderivatives of even very complicated expressions.
Remarkably, the First Fundamental Theorem of Integral Calculus
asserts that in order to calculate the integral of a function f(x) between two
points a and b, we need only evaluate its antiderivative F(x) at those
two points, and subtract them!
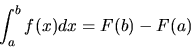 |
(39) |


Next: Differential Equations and Computational
Up: No Title
Previous: Taylor Series
Neil Dodgson
2000-10-23
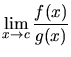
![$\displaystyle \frac{\lim_{x \rightarrow c}
[f(x)]}{\lim_{x \rightarrow c}[g(x)]} \; \; {\rm assuming } \; \;
(\lim_{x \rightarrow c}[g(x)] \ne 0)$](img51.gif)
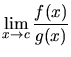
![$\displaystyle \frac{\lim_{x \rightarrow c}
[f(x)]}{\lim_{x \rightarrow c}[g(x)]} \; \; {\rm assuming } \; \;
(\lim_{x \rightarrow c}[g(x)] \ne 0)$](img51.gif)
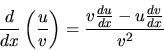
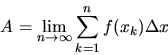
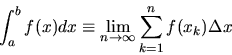
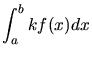
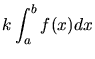
![$\displaystyle \int_{a}^{b} [ f(x) + g(x)] dx$](img75.gif)
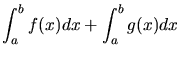
![$\displaystyle \int_{a}^{b} [ f(x) - g(x)] dx$](img77.gif)
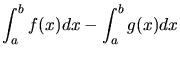
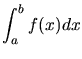
![$\displaystyle \int_{a}^{b} g(x) dx \; \; {\tt if} \; \; f(x) \le g(x)
\; \; {\tt on} \; \; [a,b]$](img81.gif)