Differential Equations and Computational Ways to Solve Them

A vast variety of phenomena that one may wish to model are described in terms of differential equations: algebraic relationships among variables and various orders of their derivatives. The goal is to find the function which satisfies a given differential equation: that function for which the stated relationship among its derivatives etc. is true. Such a function is called a solution to the differential equation. For example, the first-order differential equation

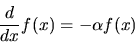$$\frac{d}{dx}f(x)=-\alpha f(x)$$ (40)

has the general solution

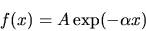$$f(x)=A\exp(-\alpha x)$$ (41)

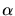(where $\alpha$ may be complex). The second-order differential equation

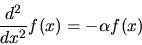$$\frac{d^{2}}{dx^{2}}f(x)=-\alpha f(x)$$ (42)

has solutions such as

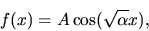$$f(x)=A\cos(\sqrt{\alpha}x),$$ (43)

or

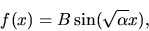$$f(x)=B\sin(\sqrt{\alpha}x),$$ (44)

or the more general combination of these sorts of solutions, the complex exponential:

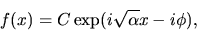$$f(x)=C \exp(i\sqrt{\alpha}x-i\phi),$$ (45)

where we may note that

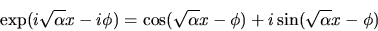$$\exp(i\sqrt{\alpha}x-i\phi) = \cos(\sqrt{\alpha}x-\phi) + i \sin(\sqrt{\alpha}x-\phi)$$ (46)

Often the solution to a differential equation depends upon initial conditions, or boundary conditions. Sometimes an exact analytic solution can be found, but more generally there is no simple expression for the solution in terms of familiar functions. Rather, one must numerically solve the differential equation by writing a program which integrates it, step by step along its variables beginning with the initial conditions. This is one of the major topics of Numerical Analysis.

Solving a differential equation (or a coupled family of differential equations) numerically involves the same operations as computing a definite integral by taking the limit of a sum of small rectangles. (That is called Euler's method.) In this respect, computing numerical solutions to differential equations is essentially an exercise in judicious extrapolation. The performance of an algorithm is gauged by its accuracy and its stability when the true solution is rapidly changing; different approaches are needed for different classes of differential equations. We can do better by using local estimators other than the rectangles that we think about as underlying integration when we pass to the limit of infinitesimals. The key issue here is the trade-off between round-off error (which can propagate nastily), and stepsize (i.e. the width of the rectangles), which is denoted h.

• Euler method: next value equals the previous value, plus some stepsize times the derivative at the previous point:
  

  $$f(x_{k+1}) \approx f(x_{k}) + h f'(x_{k})$$ (47)

  
  
  The accumulated error $\epsilon$is proportional to stepsize: $\epsilon \approx {\cal O} (h)$.
• Improved Euler Method: next value equals the previous value, plus some stepsize times the average of the previous value of the derivative and its estimated next value. Error behaviour: accumulated error is proportional to the square of the stepsize: $\epsilon \approx {\cal O} (h^{2})$.
• Simpson's Method: Use a linear combination of estimates at three points, in an overlapping 1:4:1 sequence. Error behaviour: $\epsilon \approx {\cal O} (h^{3})$.
• Runge-Kutta Method: Propagate a solution over an interval by combining the information from several Euler-style steps, and then use this information to match a Taylor series expansion up to some specified order (usually 2nd or 4th order terms). Thus the estimate of the solution to the differential equation at any point is a linear combination of these evaluated differentials. Error behaviour: $\epsilon \approx {\cal O} (h^{4})$.
• Hamming's Predictor-Corrector Method: Examine the recent behaviour of the solution (up to the present point) to make a prediction about the near-term future behaviour, and then correct this prediction using the differential information. Error behaviour: $\epsilon \approx {\cal O} (h^{5})$.

Numerical instability is the bogey-man when integrating families of differential equations numerically, especially if they happen to be nonlinear or semi-pathological (local behaviour resembling singularities). If the stepsize is too large, then there is gross quantization error. If the stepsize is made too small, then besides the greater computational cost of having to make many more calculations, numerical instability can result from propagation of truncation errors, and the solution is said to ``blow-up" (i.e. become unbounded and fail to represent the true solution).

The relationship between the cumulative error 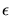$\epsilon$ and the stepsize h varies from linear dependence on h for the Euler method, to the fifth power of h for the predictor-corrector method! This reveals the great advantage of choosing a clever method for numerical integration: reducing the stepsize of integration by half can yield a 32-fold reduction in the cumulative error.

To integrate numerically an entire family of coupled differential equations, cycle iteratively through the family, one increment at a time to produce each new estimate of the solution for each member of the family. These new estimates for the whole family at that point are then used in calculating the next differential increment to the solution for each member, and the cycle repeats in a new iteration. Clearly, the fact that the solution to all the equations is required at one point before any of them can be solved at the next point, implies that such numerical solutions are profoundly serial and thus generally not amenable to the exploitation of parallel computing architectures across the evolution of the solution. However, parallelism can be exploited across the members of the family of equations, with data sharing about the outcome of each successive solution point for each member of the coupled family.