Taylor Series

A particularly powerful and remarkable way to expand a function is simply to use all of its derivatives at some fixed, known, point. It should seem surprising to you that just having complete knowledge about the function at one point, allows you to predict what its value will be at all other points!!

The terms of such an expansion of the function f(x) are based on the successive derivatives of the function at the fixed known point a, denoted f'(a), f'' (a), and so forth, each of which is then multiplied by the corresponding power function of the difference between a and the point x at which we desire to know the value of f(x). This is called a Taylor series, and if we consider just the first n terms of such an expansion, then we have an approximation up to order n of f(x), which will be denoted f_n(x):

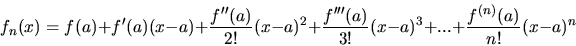$$f_{n}(x)=f(a) + f' (a)(x-a) + \frac{f'' (a)}{2!}(x-a)^{2} + \... ...{f''' (a)}{3!}(x-a)^{3} + ... + \frac{f^{(n)}(a)}{n!}(x-a)^{n}$$ (13)