


Next: Taylor Series
Up: No Title
Previous: Expansions and Basis Functions
If the chosen basis functions satisfy the rule that the integral of the
conjugate product of any two different members of the family equals zero,
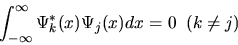 |
(9) |
then this family of functions is called orthogonal.
The above integral is called an inner product, and it is often
denoted by putting the two functions inside angle brackets (conjugation
of one of them is implied:)
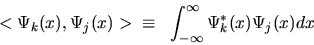 |
(10) |
If it is also true that the inner product of any member of this family
of functions with itself is equal to 1,
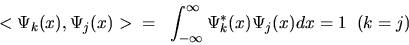 |
(11) |
then these functions are said to be orthonormal. If they form a
complete basis, then all of the coefficients ak that are needed
to represent some arbitrary function f(x) exactly in terms of the chosen
family of orthonormal basis functions
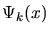 can be obtained just
by taking the inner products of the original function f(x) with each of
the basis functions
can be obtained just
by taking the inner products of the original function f(x) with each of
the basis functions
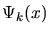 :
:
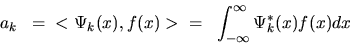 |
(12) |
One example of such a representation is the Fourier Transform, which we
will examine later.



Next: Taylor Series
Up: No Title
Previous: Expansions and Basis Functions
Neil Dodgson
2000-10-23