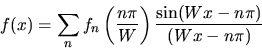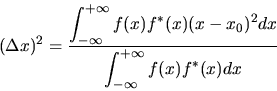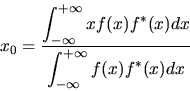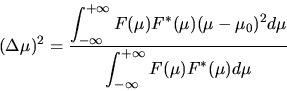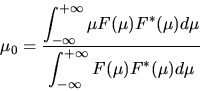

Next: About this document ...
Up: No Title
Previous: Fourier Analysis
Subsections
There are several important results in continuous mathematics
expressing the idea that even though
a function (such as some time-varying signal)
is continuous and dense in time (i.e. the value of the signal is
defined at each real-valued moment in time), nevertheless a finite and
countable set of discrete numbers suffices to describe it completely,
and thus to reconstruct it, provided that its frequency bandwidth is limited.
Such theorems may seem counter-intuitive at first: How could a finite
sequence of numbers, at discrete intervals, capture
exhaustively the continuous and uncountable stream of numbers that represent
all the values taken by a signal over some interval of time?
In general terms, the reason is that bandlimited continuous functions
are not as free to vary as they might at first seem. Consequently,
specifying their values at only certain points, suffices to determine
their values at all other points.
Figure 2:
The sinc function for recovering a continuous signal exactly from
its discrete samples, provided their frequency equals the Nyquist rate.
|
Some examples are:
- Nyquist's Sampling Theorem: If a signal f(x) is
strictly bandlimited so that it contains no frequency components higher
than W, i.e. its Fourier Transform
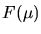 satisfies the condition
satisfies the condition
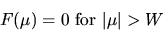 |
(69) |
then f(x) is completely determined just by sampling its values at a
rate of at least 2W. The signal f(x) can be exactly recovered by
using each sampled value to fix the amplitude of a sinc(x) function,
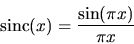 |
(70) |
whose width is scaled by the bandwidth parameter W and whose location
corresponds to each of the sample points. The continuous signal f(x)can be perfectly recovered from its discrete samples
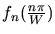 just by adding all of those displaced sinc(x) functions together, with their
amplitudes equal to the samples taken:
just by adding all of those displaced sinc(x) functions together, with their
amplitudes equal to the samples taken:
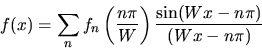 |
(71) |
(The Figure illustrates this function.)
Thus, any signal that is limited in its
bandwidth to W, during some duration Thas at most 2WT degrees-of-freedom. It can be completely
specified by just 2WT real numbers!
- The Information Diagram: The Similarity Theorem
of Fourier Analysis asserts that if a function becomes narrower in one
domain by a factor a, it necessarily becomes broader by the same
factor a in the other domain:
 |
(72) |
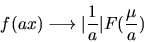 |
(73) |
The Hungarian Nobel-Laureate Dennis Gabor took this principle further
with great insight and with implications that are still revolutionizing
the field of signal processing (based upon wavelets), by noting that an
Information Diagram representation of signals in a plane defined by
the axes of time and frequency is fundamentally quantized.
There is an irreducible, minimal, volume that any signal can
possibly occupy in this plane. Its uncertainty (or spread) in frequency,
times its uncertainty (or duration) in time, has an inescapable lower bound.
If we define the ``effective support" of a function f(x) by its
normalized variance,
or the normalized second-moment
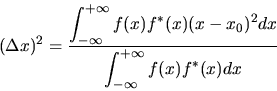 |
(74) |
where x0 is the mean value, or first-moment, of the function
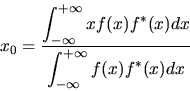 |
(75) |
and if we similarly define the effective support of the Fourier Transform
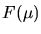 of the function by its normalized variance in the Fourier domain
of the function by its normalized variance in the Fourier domain
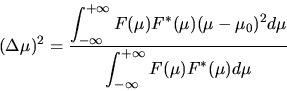 |
(76) |
where 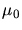 is the mean value, or first-moment, of the Fourier transform
is the mean value, or first-moment, of the Fourier transform
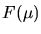
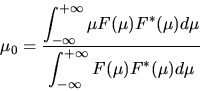 |
(77) |
then it can be proven (by Schwartz Inequality arguments) that there exists
a fundamental lower bound on the product of these two ``spreads,"
regardless of the function f(x) !
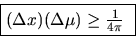 |
(78) |
This is the famous Gabor-Heisenberg-Weyl Uncertainty Principle.
Mathematically it is exactly identical to the uncertainty relation in
quantum physics, where
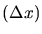 would be interpreted as the position
of an electron or other particle, and
would be interpreted as the position
of an electron or other particle, and
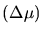 would be interpreted as
its momentum or deBroglie wavelength. We see that this is not just a
property of nature, but more abstractly a property of all functions and
their Fourier Transforms. It is thus a still further, and more lofty,
respect in which the information in continuous signals is quantized,
since they must occupy an area in the Information Diagram (time -
frequency axes) that is always greater than some irreducible lower bound.
would be interpreted as
its momentum or deBroglie wavelength. We see that this is not just a
property of nature, but more abstractly a property of all functions and
their Fourier Transforms. It is thus a still further, and more lofty,
respect in which the information in continuous signals is quantized,
since they must occupy an area in the Information Diagram (time -
frequency axes) that is always greater than some irreducible lower bound.
Dennis Gabor named such minimal areas ``logons" from the Greek word for
information, or order: logos. He thus established that the Information
Diagram for any continuous signal can contain only a fixed number of
information ``quanta." Each such quantum constitutes an independent datum,
and their total number within a region of the Information Diagram
represents the number of independent degrees-of-freedom enjoyed by the
signal.
The unique family of signals that actually achieve the lower bound in
the Gabor-Heisenberg-Weyl Uncertainty Relation are the complex
exponentials multiplied by Gaussians. These are sometimes referred to
as ``Gabor wavelets:"
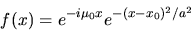 |
(79) |
localized at ``epoch" x0, modulated by frequency 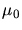 , and with
size or spread constant a. It is noteworthy that such wavelets have
Fourier Transforms
, and with
size or spread constant a. It is noteworthy that such wavelets have
Fourier Transforms 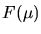 with exactly the same functional form, but
with their parameters merely interchanged or inverted:
with exactly the same functional form, but
with their parameters merely interchanged or inverted:
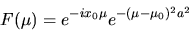 |
(80) |
Note that in the case of a wavelet (or wave-packet) centered on x0=0,
its Fourier Transform is simply a Gaussian centered at the modulation
frequency 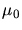 , and whose size is 1/a, the reciprocal of the wavelet's
space constant.
, and whose size is 1/a, the reciprocal of the wavelet's
space constant.
Because of the optimality of such wavelets under the Uncertainty Principle,
Gabor (1946) proposed using them as an expansion basis to represent signals.
In particular, he wanted them to be used in broadcast telecommunications
for encoding continuous-time information. He called them the ``elementary
functions" for a signal. Unfortunately, because such functions are mutually
non-orthogonal, it is very difficult to obtain the actual
coefficients needed as weights on the elementary functions in order to
expand a given signal in this basis! The first constructive method for
finding such ``Gabor coefficients" was developed in 1981 by the Dutch physicist
Martin Bastiaans, using a dual basis and a complicated
non-local infinite series.
When a family of such functions are parameterized
to be self-similar, i.e. they are dilates and translates of each other so
that they all have a common template (``mother" and ``daughter"), then
they constitute a (non-orthogonal) wavelet basis. Today it is known
that an infinite class of wavelets exist which can be used as the expansion
basis for signals. Because of the self-similarity property, this amounts
to representing or analyzing a signal at different scales.
This general field of investigation is called multi-resolution analysis.
Two-dimensional Gabor filters over the image domain (x,y) have
the functional form
![\begin{displaymath}f(x,y)=e^{-\left[(x-x_{0})^{2}/\alpha^{2} + (y-y_{0})^{2}/\beta^{2}\right]}
e^{-i\left[u_{0}(x-x_{0}) + v_{0}(y-y_{0})\right]}
\end{displaymath}](img186.gif) |
(81) |
where
(x0,y0) specify position in the image,
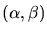 specify
effective width and length, and
(u0,v0) specify modulation,
which has spatial frequency
specify
effective width and length, and
(u0,v0) specify modulation,
which has spatial frequency
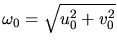 and direction
and direction
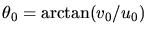 .
(A further degree-of-freedom
not included above is the relative orientation of the
elliptic Gaussian envelope, which creates cross-terms in xy.)
The 2-D Fourier transform F(u,v) of a 2-D Gabor
filter has exactly the same functional form, with parameters just
interchanged or inverted:
.
(A further degree-of-freedom
not included above is the relative orientation of the
elliptic Gaussian envelope, which creates cross-terms in xy.)
The 2-D Fourier transform F(u,v) of a 2-D Gabor
filter has exactly the same functional form, with parameters just
interchanged or inverted:
![\begin{displaymath}F(u,v)=e^{-\left[(u-u_{0})^{2}\alpha^{2} + (v-v_{0})^{2}\beta^{2}\right]}
e^{-i\left[x_{0}(u-u_{0}) + y_{0}(v-v_{0})\right]}
\end{displaymath}](img189.gif) |
(82) |
2-D Gabor functions can form a complete self-similar 2-D wavelet expansion
basis, with the requirements of orthogonality and strictly compact
support relaxed, by appropriate parameterization for
dilation, rotation, and translation. If we take 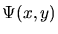 to be a chosen
generic 2-D Gabor wavelet, then we can generate from this one member a
complete self-similar family of 2-D wavelets through the generating function:
to be a chosen
generic 2-D Gabor wavelet, then we can generate from this one member a
complete self-similar family of 2-D wavelets through the generating function:
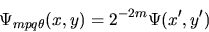 |
(83) |
where the substituted variables (x',y') incorporate
dilations in size by 2-m, translations
in position (p,q), and rotations through orientation 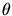 :
:
![\begin{displaymath}x'=2^{-m}[x\cos(\theta) + y\sin(\theta)]-p
\end{displaymath}](img192.gif) |
(84) |
![\begin{displaymath}y'=2^{-m}[-x\sin(\theta)+y\cos(\theta)]-q
\end{displaymath}](img193.gif) |
(85) |
It is noteworthy that as consequences of the similarity theorem, shift
theorem, and modulation theorem of 2-D Fourier analysis, together with the
rotation isomorphism of the 2-D Fourier transform, all of these effects of
the generating function applied to a 2-D Gabor mother wavelet
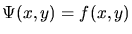 have corresponding identical or reciprocal
effects on its 2-D Fourier transform F(u,v). These properties of
self-similarity can be exploited when constructing efficient,
compact, multi-scale codes for
image structure.
Now we can
see that the ``Gabor domain" of representation actually embraces and unifies
both the Fourier domain and the original signal domain!
To compute the representation of a signal or of data in the
Gabor domain, we find its expansion in terms of elementary functions
having the form
have corresponding identical or reciprocal
effects on its 2-D Fourier transform F(u,v). These properties of
self-similarity can be exploited when constructing efficient,
compact, multi-scale codes for
image structure.
Now we can
see that the ``Gabor domain" of representation actually embraces and unifies
both the Fourier domain and the original signal domain!
To compute the representation of a signal or of data in the
Gabor domain, we find its expansion in terms of elementary functions
having the form
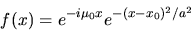 |
(86) |
The single parameter a (the space-constant in the Gaussian
term) actually builds a continuous bridge between
the two domains: if the parameter a is made very large, then the second
exponential above approaches 1.0, and so in the limit
our expansion basis becomes
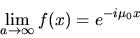 |
(87) |
the ordinary Fourier basis! If the parameter a is instead made very small,
the Gaussian term becomes the approximation to a delta function at location
xo, and so our expansion basis implements pure space-domain sampling:
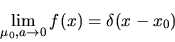 |
(88) |
Hence the Gabor expansion basis ``contains" both domains at once. It
allows us to make a continuous deformation
that selects a representation lying anywhere on a one-parameter continuum
between two domains that were hitherto distinct and mutually unapproachable.
A new Entente Cordiale, indeed.


Next: About this document ...
Up: No Title
Previous: Fourier Analysis
Neil Dodgson
2000-10-23