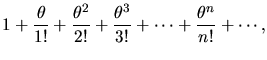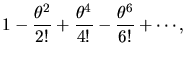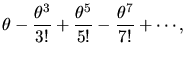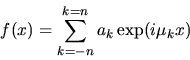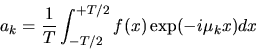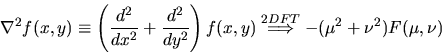Let function f(x) have Fourier
Transform
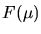 ,
and let function g(x) have Fourier Transform
,
and let function g(x) have Fourier Transform 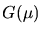 .
The
convolution of f(x) with g(x), which is denoted f*g,
combines these two functions to generate a third function
h(x), whose value at location (x) is equal to the integral of the
product of functions f and g after they undergo a relative shift
by amount (x):
.
The
convolution of f(x) with g(x), which is denoted f*g,
combines these two functions to generate a third function
h(x), whose value at location (x) is equal to the integral of the
product of functions f and g after they undergo a relative shift
by amount (x):
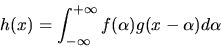 |
(57) |
Thus, convolution is a way of combining two functions, in a sense using each one
to blur the other, making all possible relative shifts between the two functions
when computing the integral of their product to obtain the corresponding output
values.
Convolution is extremely important because it is one basis of describing how
any linear system h(t) acts on any input s(t) to generate the corresponding
output r(t). Specifically, the output is just the convolution of the input
with the characteristic system response function:
The Convolution Theorem
states that convolving any two functions f(x) and
g(x) together simply multiplies their
two Fourier Transforms together, to generate the Fourier Transform of the
result of the convolution:
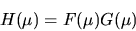 |
(59) |
where 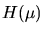 is the Fourier Transform of the desired result h(x),
and
is the Fourier Transform of the desired result h(x),
and 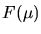 and
and 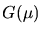 are the Fourier Transforms of f(x) and g(x),
respectively.
are the Fourier Transforms of f(x) and g(x),
respectively.
This is extremely useful since it is much easier to multiply two
functions 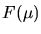 and
and 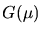 together, to obtain
together, to obtain 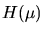 ,
than to convolve f(x) and g(x) together to obtain h(x).
Of course, exploiting the Convolution Theorem means going into the
Fourier Domain and computing the Fourier Transforms of f(x) and g(x),
but with
powerful and fast FFT algorithms, this is very easy.
,
than to convolve f(x) and g(x) together to obtain h(x).
Of course, exploiting the Convolution Theorem means going into the
Fourier Domain and computing the Fourier Transforms of f(x) and g(x),
but with
powerful and fast FFT algorithms, this is very easy.