


Next: Solution Notes
Up: Continuous Mathematics
Previous: Solution Notes
- 1.
- Member of this family of wavelets are self-Fourier, because
they have exactly the same functional form as their Fourier Transforms.
Just their parameters are interchanged or inverted in the functional form
in the two domains.
- 2.
- The modulation parameter
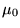 in f(x) becomes the location
parameter of the wavelet
in f(x) becomes the location
parameter of the wavelet 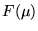 which is its Fourier transform. The
position parameter x0 of wavelet f(x) becomes the modulation parameter
of the wavelet
which is its Fourier transform. The
position parameter x0 of wavelet f(x) becomes the modulation parameter
of the wavelet 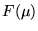 which is its Fourier transform. Hence modulation
and shifting are dual. Finally, the scale parameter
which is its Fourier transform. Hence modulation
and shifting are dual. Finally, the scale parameter 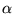 sets the
size of the wavelet f(x), and the reciprocal of
sets the
size of the wavelet f(x), and the reciprocal of 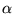 is the size
of the wavelet
is the size
of the wavelet 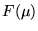 which is the Fourier transform of f(x); this
expresses the duality of scaling (``similarity").
which is the Fourier transform of f(x); this
expresses the duality of scaling (``similarity").
- 3.
- The Fourier transform of the sum of any two Gabor wavelets is itself the
sum of two Gabor wavelets.
- 4.
- The Fourier transform of the product of any two Gabor wavelets is a
single Gabor wavelet.
This is because the product of any two Gabor wavelets
is itself just a new Gabor wavelet (the arguments of the exponentials simply
add within each exponential), and the conclusion then follows from (1).
- 5.
- The Fourier transform of
f(n)(x), the nth-derivative of a Gabor
wavelet, is:
- 6.
- The duality of convolution and multiplication implies that the convolution
of any two Gabor wavelets has a Fourier transform which is the product of two
Gabor wavelets. But we noted above in (4) that such a product is just a single
Gabor wavelet. Combining this result with the self-Fourier property, we conclude
that the convolution of any two Gabor wavelets is itself, yet again, just a
single Gabor wavelet.
Hence this family of functions is closed under convolution, just as it is
under multiplication.



Next: Solution Notes
Up: Continuous Mathematics
Previous: Solution Notes
Neil Dodgson
2000-10-20