Solution Notes -- Example Problem Set 7

1.

The duality of convolution and multiplication implies that if two functions are convolved, the Fourier transform of their result is the product of their respective Fourier transforms:

$$h(x) = f(x)*g(x) \stackrel{FT}{\Longrightarrow} H(\mu)=F(\mu)G(\mu)$$

where * denotes convolution, and $F(\mu)$, $G(\mu)$, and $H(\mu)$ are the respective Fourier transforms of f(x), g(x), and h(x).

Similarly, if two functions are multiplied together, the Fourier transform of their product is the convolution of their respective Fourier transforms:

$$h(x) = f(x)g(x) \stackrel{FT}{\Longrightarrow} H(\mu)=F(\mu)*G(\mu)$$

Closure of the family of functions under multiplication means that h(x)= f(x)g(x) will have the same functional form as f(x) and g(x). Therefore $H(\mu)=F(\mu)*G(\mu)$ will also have the same functional form as $F(\mu)$ and $G(\mu)$. Since these functions are self-Fourier, it follows that closure under multiplication entails closure under convolution. The same argument can be applied in the reverse direction.

2.

Since the square wave is just the first derivative of the triangular wave, we can expand the differentiation across all the terms in the expansion series and demand that the Fourier series for the square wave consists of term-wise derivatives of the Fourier series for the triangular wave. This tells us that the triangular wave Fourier series must be:

$$f(x)= \sum_{{\rm odd \ }n=1}^{\infty} -\frac{1}{n^{2}} \cos(nx)$$

3.

Additivity of Fourier transforms tells us that the FT of f(x) equals the FT of f_e(x) plus the FT of f_o(x).

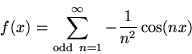
Since f_e(x) has even symmetry, its FT is purely real (i.e. the imaginary part of all Fourier coefficients is 0), because the integral of the product of an even function times an odd function is 0. Similarly, the FT of f_o(x) is purely imaginary, because (again) the integral of the product of any odd function times an even function is 0, so the real-part is 0.

Thus a real-valued function has an FT whose real part has even symmetry, and whose imaginary part has odd symmetry. This is Hermitian symmetry.

The computational advantage which can be exploited is that for real-valued data, we need only compute the Fourier transform over the positive frequencies. The coefficients we get will automatically tell us the corresponding coefficients for the negative frequencies. So we need only compute half as many numbers as we would have needed to compute if the data had been complex rather than real.