Solution Notes -- Example Problem Set 6

1.

Gabor wavelets are defined as the following 3-parameter functions:

$$f(x)=e^{-i \mu_{0} x} e^{-(x-x_{0})^{2}/a^{2} }$$

The meanings of the three parameters are: localization at ``epoch" x₀, modulation by frequency $\mu_{0}$, and wavelet size or spread constant a.

2.

Gabor-Heisenberg-Weyl Uncertainty Relation. If we define the ``effective support" of a function f(x) by its normalized variance, or the normalized second-moment

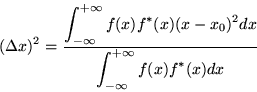$$(\Delta x)^{2} = \frac{\displaystyle \int_{-\infty}^{+\infty}... ... dx} {\displaystyle \int_{-\infty}^{+\infty} f(x) f^{*}(x) dx}$$ (1)

where x₀ is the mean value, or first-moment, of the function

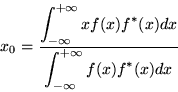$$x_{0} = \frac{\displaystyle \int_{-\infty}^{+\infty} x f(x) f... ... dx} {\displaystyle \int_{-\infty}^{+\infty} f(x) f^{*}(x) dx}$$ (2)

and if we similarly define the effective support of the Fourier Transform $F(\mu)$ of the function by its normalized variance in the Fourier domain

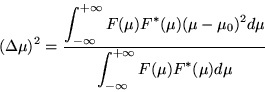$$(\Delta \mu)^{2} = \frac{\displaystyle \int_{-\infty}^{+\inft... ...\displaystyle \int_{-\infty}^{+\infty} F(\mu) F^{*}(\mu) d\mu}$$ (3)

where $\mu_{0}$ is the mean value, or first-moment, of the Fourier transform $F(\mu)$

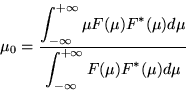$$\mu_{0} = \frac{\displaystyle \int_{-\infty}^{+\infty} \mu F(... ...\displaystyle \int_{-\infty}^{+\infty} F(\mu) F^{*}(\mu) d\mu}$$ (4)

then it can be proven (by Schwartz Inequality arguments) that there exists a fundamental lower bound on the product of these two ``spreads," regardless of the function f(x)

$$\fbox{$(\Delta x) (\Delta \mu) \ge \frac{1}{4 \pi} $\space }$$ (5)

This is the Gabor-Heisenberg-Weyl Uncertainty Principle, and the unique family of signals that actually achieve its lower bound are the complex exponentials multiplied by Gaussians. These are the ``Gabor wavelets."

3.

The smallest possible area that any function can occupy in the Information Diagram is: $(\Delta x) (\Delta \mu) = \frac{1}{4 \pi}$. Gabor wavelets, regardless of their parameter values, always achieve this lower bound on area. Their shapes may of course differ, as the diagram shows, but their jointly occupied areas are always equal. All other functions will occupy areas larger than this in the Information Diagram, and thus have less sharp information resolution.

4.

To compute the representation of a signal or of data in the Gabor domain, we find its expansion in terms of elementary functions having the form

$$f(x)=e^{-i \mu_{0} x} e^{-(x-x_{0})^{2}/a^{2} }$$ (6)

The single parameter a (the space-constant in the Gaussian term) actually builds a continuous bridge between the time domain and the Fourier domain: if the parameter a is made very large, then the second exponential above approaches 1.0, and so in the limit our expansion basis becomes

$$\lim_{a \rightarrow \infty} f(x)=e^{-i \mu_{0} x}$$ (7)

the ordinary Fourier basis. If the parameter a is instead made very small, the Gaussian term becomes the approximation to a delta function at location x_o, and so the expansion basis implements (if we set $\mu_{0}$ to 0) pure space-domain sampling:

$$\lim_{\mu_{0},a \rightarrow 0} f(x)=\delta(x-x_{0})$$ (8)

Hence the Gabor expansion basis ``contains" both domains at once. It allows us to make a continuous deformation that selects a representation lying anywhere on a one-parameter continuum between two domains that were hitherto distinct and mutually unapproachable. The price paid for this unification of the two domains is that the new expansion basis is, in general, non-orthogonal. This makes it much more difficult to obtain the coefficients for the expansion.