Solution Notes -- Example Problem Set 5

1.

By taking the Fourier Transform of both sides of the differential equation, and by exploiting the fact that this is a linear operation and using the Differentiation Theorem of Fourier analysis, we arrive at the following equation in the frequency domain:

$$A (i \mu)^{2} F(\mu) + B i \mu F(\mu) = G(\mu)$$

from which it follows that the Fourier Transform of the solution we seek is simply

$$F(\mu) = \frac{G(\mu)}{iB \mu - A\mu^{2}}$$

Finally, we need to compute the inverse Fourier Transform of 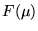$F(\mu)$, and this will give us the solution f(x) that we seek for the differential equation.

2.

It requires N+1 consecutive sample points in order to calculate the 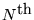$N^{\mbox{th}}$ derivative of a function in a region.

The weights which need to be multiplied by consecutive samples of the function in order to calculate its 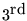$3^{\mbox{rd}}$ derivative are: -1, +3, -3, +1.

3.

The principal advantage is that if orthogonal functions are used, then the expansion coefficients which give the representation of the function (or data) in terms of the universal basis functions are obtained merely by inner product projection. (A normalization factor would also be required if the basis functions were orthogonal but not orthonormal.) If we used functions that were non-orthogonal, then a great deal more linear algebra would be required in order to obtain their desired coefficients.

We must compute the inner product or projection of 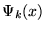$\Psi_{k}(x)$ and f(x), which will give us each basis coefficient a_k:

$$a_{k} \; \; = \; \; < \Psi_{k}(x), f(x) > \; \; = \; \; \int_{-\infty}^{\infty} \Psi_{k}^{*} (x) f(x) dx$$