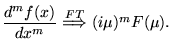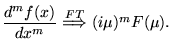

Next: Solution Notes
Up: Continuous Mathematics
Previous: Solution Notes
- 1.
- The new Fourier Transform will be:
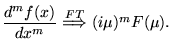
- 2.
- The new Fourier Transform will be:
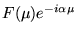 .
.
- 3.
- The new Fourier Transform will be:
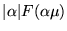 .
.
- 4.
- The Fourier Transform
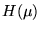 of the convolution result h(x) from
convolving f(x) with another function g(x), having respective Fourier
Transforms
of the convolution result h(x) from
convolving f(x) with another function g(x), having respective Fourier
Transforms 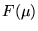 and
and 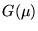 ,
is the product of the two
Transforms:
,
is the product of the two
Transforms:
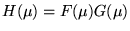 .
.
- 5.
- The Laplacian operator
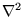 is defined as:
is defined as:
and the 2D Fourier Transform of
 is:
is:
Neil Dodgson
2000-10-20