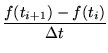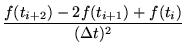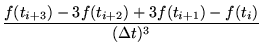Next: Solution Notes
Up: Continuous Mathematics
Previous: Solution Notes
- 1.
- Prediction is
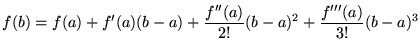 (A Taylor series which in effect gives a polynomial expansion of f(t)around t=a, in terms of derivatives of successive powers of t.)
(A Taylor series which in effect gives a polynomial expansion of f(t)around t=a, in terms of derivatives of successive powers of t.)
- 2.
-
There are alternative, equally valid answers, which use the symmetric
approximation to the derivatives.
- 3.
- If we use
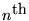 -order Runge-Kutta then the error in a
given step will depend upon the step size raised to the
-order Runge-Kutta then the error in a
given step will depend upon the step size raised to the
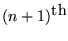 power, while the accumulated error will depend upon
the step size raised to the
power, while the accumulated error will depend upon
the step size raised to the
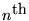 power
power
- 4.
- When computing its
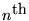 -order derivative, the noise
in the signal is amplified as the
-order derivative, the noise
in the signal is amplified as the
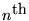 -power of frequency.
Thus for the cases given and for frequency
-power of frequency.
Thus for the cases given and for frequency 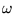 ,
this noise
problem will grow as
,
this noise
problem will grow as
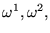 and
and
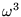 ,
respectively.
,
respectively.



Next: Solution Notes
Up: Continuous Mathematics
Previous: Solution Notes
Neil Dodgson
2000-10-20
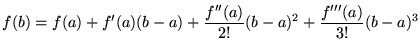 (A Taylor series which in effect gives a polynomial expansion of f(t)around t=a, in terms of derivatives of successive powers of t.)
(A Taylor series which in effect gives a polynomial expansion of f(t)around t=a, in terms of derivatives of successive powers of t.)