Solution Notes -- Example Problem Set 2

1.

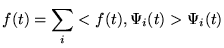$f(t)={\displaystyle \sum_{i}<f(t), \Psi_{i}(t)> \Psi_{i}(t)}$ie, a linear combination of all the basis functions 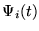$\Psi_{i}(t)$, each weighted by a coefficient giving the projection (inner product) of f(t)onto that basis function.

2.

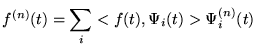$f^{(n)}(t)={\displaystyle \sum_{i}<f(t), \Psi_{i}(t)> \Psi_{i}^{(n)}(t)}$ie, a linear combination of the nth derivatives of the basis functions, 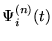$\Psi_{i}^{(n)}(t)$, each weighted by a coefficient giving the projection (inner product) of f(t)onto the original non-differentiated basis function.

3.

The output r(t) must also be a complex exponential, differing from the input one only by some complex coefficient (say $\alpha$): $r(t)=\alpha e^{i\mu_{j}t}$

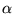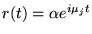
4.

No. Complex exponentials are the eigenfunctions of linear time-invariant systems. Therefore such inputs are unchanged in their functional form when they appear as outputs as a result of being processed by the system.