(A) (i): When numerically computing the solution to an ODE
that involves higher-than first-order derivatives, the higher-order
terms must be reduced to 1st-order terms. This can be accomplished
by introducing new substituted variables such as
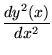 .
.
(ii) Thus the example ODE,
(B) (i) The incrementing rule for the Euler method of numerical
integration is:
(ii) If the stepsize h is too large, this piecewise-linear approximation to the solution will be inaccurate where the true solution has significant second derivatives (which this method ignores). The solution may ``blow up."
(iii) If the stepsize h is made too small, the computation may take too long and the round-off error (truncation of floating-point numbers depending on the word length of the machine) will accumulate too much, making the solution inaccurate or even unstable.
(iv) The primary advantage of the fourth-order Runge-Kutta method over the Euler method for numerical integration of ODEs is that its accumulated error depends on the stepsize h as its 4th power, h4, whereas in the Euler method the accumulated error is simply linear in h. Thus, for example, reducing the stepsize h by half would only reduce the accumulated error by half in the Euler method, but it would reduce it 16-fold in the Runge-Kutta method.