
Abstract. It’s very hard – maybe impossible – to achieve unassailable proof of the security of the hardware and software making up computer systems like PCs or servers. Perhaps there’s hope of proving properties of a tiny system? MITB, the result of a collaboration with Graham Steel and Robert Künnemann, is incredibly tiny, but even it turned out to be challenging. What follows incorporates comments and text from Robert.
The “MAC In The Box” project – “MITB” for short – was thought up by Graham Steel following conversations on ways that he and I might collaborate. The name, also devised by Graham, derives from “HMAC”, as the eventual goal was to design and formally verify hardware and software implementing a device to hash passwords and other security critical data. The idea was to explore plugging a gap in existing security arguments for storing hash parameters in separate hardware: for example, the formal analysis of the Yubikey protocol by Künnemann and Steel assumes “that the implementation is correct with respect to the documentation” (see Slide 9 of this talk). To reduce risks inherent in this assumption, the project aimed to build and verify a hashing application running on a server and a physically separate simple hardware token that could create password hashes using parameters stored securely on the device.
Graham, his then PhD student Robert Künnemann, I and others initially made fast progress. However, after a while the project slowly ground to a halt, but a lot was achieved before this happened.
The sections below provide further details and discussion of what was and wasn’t achieved. I think the goals of the MITB project are still timely and scientifically challenging, so I hope the project might someday be revived.
This article reorganises and updates text extracted from the old MITB web pages at http://www.cl.cam.ac.uk/~mjcg/MITB/ into a single document. The security proofs done by Robert are online at https://github.com/CakeML/mitb.
At the 2011 FMATS workshop, Graham gave a talk showing that the operations of many crypto tokens that provide access to their functionality – their APIs – had unexpected insecurities that could be automatically found using his Tookan tool. Here are some example tokens that Tookan found insecurities in.

The ideas underlying Tookan built on earlier work such as that by Clulow and Bond & Clulow. To complement research on breaking existing tokens, the first idea for a project was to see how easy would it be to design hardware token implementations that could be mathematically proved to be unbreakable using Tookan-like tools. It was hoped to combine the API-cracking expertise of Steel’s group at INRIA with the formal verification expertise of Cambridge. Initially, an ambitious project to verify a full PKCS #11 hardware security token was planned. This early vision was outlined in an old Prezi talk I presented at an event in Chicago to honour Dave MacQueen’s retirement. Here is the first slide.

“Cryptoki” is short for “cryptographic token interface”, the PKCS\(~\)#11 standard that specifies APIs for devices holding cryptographic information and performing cryptographic functions. It was intended that the token would run a verified CakeML program implementing the Cryptoki API.
Over the next year or so, this goal evolved into the much less ambitious MITB project, which aims to be a proof-of-concept first step.
MITB is intended to be a very simple hardware token for hashing passwords and other security critical data using the SHA-3 algorithm. Quoting from Wikipedia (https://en.wikipedia.org/wiki/SHA-3):
"SHA-3 (Secure Hash Algorithm 3), a subset of the cryptographic
primitive family Keccak ,... is a cryptographic hash function
designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles
Van Assche, building upon RadioGatún. SHA-3 is a member of the
Secure Hash Algorithm family. The SHA-3 standard was released by
NIST on August 5, 2015. The reference implementation source code
was dedicated to public domain via CC0 waiver."The plan was to verify an implementation of the simplest hashing device that we could think of. An early suggestion was for just two operations:
SETUP: a physical button on the device puts it into setup mode in which commands can read and write the stored secret parameter. Physical attacks are considered out-of-model for the scenario where this device will be deployed (connected to a server in a relatively physically secure location). The device could have a bright red LED for when it’s in setup mode and a green one for operational password authentication mode.
AUTHENTICATE: data is input to the device, which computes a hash of it using the secret parameter stored on the device, and then outputs the result. This would be used both to compute initial hashes for storing in the password file on the server and for authenticating later password uses by computing a hash that can be compared with the one in the server file.
This is informal high-level documentation. The project was to design a hardware implementation for an FPGA and to certify by machine-checked mathematical proof, that the implementation of MITB correctly implements formal documentation, including both normal and error behaviour. The main scientific challenge that arises is formulating what properties need to be proved to establish the trustworthiness of the device. These properties fall into two categories: functional correctness and security.
Functional correctness properties establish that the behaviour of the implementation, which consists of registers connected together by combinational logic, is the behaviour specified in the documentation. Cambridge has experience in verifying the functional correctness of such hardware.
The security properties of MITB aim to establish that the device protects secrets: for example, that an attacker cannot extract secret data in unexpected ways. Both the high-level documentation and the implementation need to be secure. Tookan discovers insecure combinations of documented API operations; we want MITB not to be vulnerable to Tookan-style analysis. Even if the implementation correctly implements MITB’s API it could also accidentally provide additional undesirable functionality or insecure side channels, e.g. the time taken to produce outputs might reveal information about what secret data was being manipulated. Graham and his colleagues at Inria are expert in showing that security properties do not hold of actual devices.
During the summer of 2013, Graham’s PhD student Robert Künnemann visited Cambridge for a couple of months. He produced implementations of Keccak in Standard ML (SML) and in HOL.
Robert also designed a state machine to implement MITB and an API for driving it. He suggested that a good security property to prove is that the only outputs from MITB that can be produced are hashes of strings.
I then formalised a version of Robert’s machine in the HOL4 version of higher-order logic. This was parametrised on various Keccac size parameters and a function representing the permutation component of the Keccak algorithm. He also proved that a temporal logic formalisation of the API specification is correctly implemented by the state-machine and that Robert’s security property holds.
Links to further details of what Robert and I did in 2013, together with some discussion, can be found in the 2013 progress report, which is online at http://www.cl.cam.ac.uk/~mjcg/MITB/Autumn2013Summary.html. What follows is an overview aiming to explain what was done, but without most of the formalisation and proof details:these are available in web pages available via the 2013 online progress report.
The MITB state-machine is a device with two 1-bit control inputs skip_inp, move_inp, two data inputs block_inp and size_inp, a 1-bit control output ready_out and a data output digest_out.

MITB is parametrised on three numbers \((r,c,n)\) and a permutation function \(f\). These are part of the Keccak specification: \(r\) is the bitrate, \(c\) the capacity and \(n\) the digest size. The function \(f\), also part of the Keccak specification, is a function that permutes bit-strings of length \(r+c\). An actual device would be manufactured with specific values for the parameters.
The input block_inp is \(r\)-bits wide and the output digest_out is \(n\)-bits wide. The input size_inp has sufficient bits to represent a number of size \(r\) or less.
MITB computes an HMAC for an arbitrary length message. The user splits the message into blocks of \(r\) bits. A sequence of control inputs are applied via skip_inp and move_inp to read the sequence of blocks and the number of blocks the message is split into from data inputs block_inp and size_inp, respectively. If MITB receives the correct inputs it will ‘squeeze’ the blocks into a digest, which can then be read from MITB’s data output digest_out. The control output ready_out signals when the digest has been computed. MITB contains a secret key that is used in hashing. There should be no way for an attacker to extract this key using the operations. The way MITB squeezes a message into a digest is described in more detail in the sections on the absorbing algorithm and the MITB protocol for absorbing below.
From a user’s point of view MITB can be in either of two states: Ready or Absorbing. It powers up into the Ready state. The 1-bit output ready_out indicates which state the machine is in.
MITB runs continuously after being switched on. All a user can observe (assuming tamper-resistant manufacture) are the sequences of values appearing on the outputs ready_out and digest_out, which depend on the values input via skip_inp, move_inp, block_inp and size_inp.
In the state-transition diagram below the Absorbing state in the documentation is realised in the implementation by being either in the state labelled Absorbing in the diagram or in the state labelled AbsorbEnd.
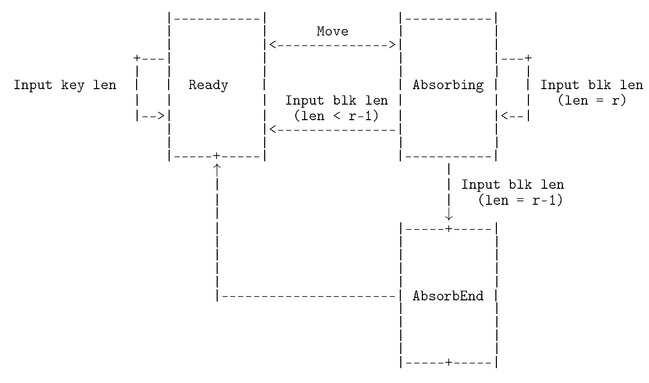
The input skip_inp ‘freezes’ MITB: it stops the state changing on successive cycles. The input move_inp causes the state to change on the next cycle; in particular it is used to signal that MITB should start absorbing a message.
The MAC of a message \(M\) is specified as the Keccak hash of the result of concatenating the secret key stored in the token onto the front of the message, i.e the hash of \(key {{\mbox{$\|$}}}M\), where \(key\) is the secret key and \({{\mbox{$\|$}}}\) is bit-string concatenation. The protocol for using MITB to compute the MAC of a message is described below. The main correctness property of the device is that if the specified protocol is used to input a message then its MAC will appear on digest_out. The functional correctness property is that no matter what inputs are supplied, the secret key cannot be revealed. These properties will be expressed as constraints on what sequences of inputs and outputs are possible, using a temporal logic notation.
MITB has a permanent memory for holding an \(r\)-bit secret key. The key can be set or changed by asserting 0 on both skip_inp and move_inp 0 in the Ready state. The data being input on block_inp then overwrites the stored key.
Keccak works by splitting a message into blocks and then `absorbing’ them.
The absorbing algorithm takes a message \(M\) as input and returns a digest \(h\). It consists of three steps: padding the input, iteratively computing a sequence of \(b\)-bit states \(s_0~\ldots~s_m\) (\(b=1600\)), extracting the digest from the final state \(s_m\). In more details the three steps are:
Apply padding to \(M\). Let the resulting blocks be \(B_1,\ldots,B_m\); each of length \(r\).
Set \(s_0=0^b\) and for \(i=1,\ldots,m\) iteratively compute \(s_i \leftarrow f(s_{i-1} {\mbox{$\oplus$}}(B_i || 0^{b-r}))\), where \(||\) is bitstring concatenation, \({\mbox{$\oplus$}}\) is bitwise XOR and \(f\) is the permutation function.
Output \(h = \lfloor s_m \rfloor_n\), where \(\lfloor s_m \rfloor_n\) is the first \(n\) bits of \(s_m\) and it is guaranteed that \(n<b\) as \(b=1600\) and \(n\in {\{\,224,256,384,512\,\}}\).
MITB is ready to compute the MAC of a message in state Ready. The protocol for computing the MAC of \(M\) is as follows (\({{\mbox{${\mid}B{\mid}$}}}\) denotes the number of bits in\(~B\)):
The user splits \(M\) into a sequence of blocks, \(M = B_1{{{\mbox{$\|$}}}} B_2{{{\mbox{$\|$}}}} \cdots {{{\mbox{$\|$}}}}B_{m-1}{{{\mbox{$\|$}}}} B_m\), such that all blocks except the last one are \(r\)-bits wide, i.e. \({{\mbox{${\mid}B_i{\mid}$}}} = r\) for \(1 \leq i < m\) and \({{\mbox{${\mid}B_m{\mid}$}}} < r\). If \(r\) divides exactly into \({{\mbox{${\mid}M{\mid}$}}}\), then \(B_n\) is taken to be the empty block (so \({{\mbox{${\mid}B_m{\mid}$}}}=0\)).
When ready_out is 1 the user puts MITB into the Absorbing state by inputting 0 on skip_inp and 1 on move_inp (block_inp and size_inp are ignored during this step).
Starting on the next cycle, and continuing for \(m\) cycles, the user inputs 0 on both move_inp and skip_inp, \(B_i\) on block_inp and \({{\mbox{${\mid}B_i{\mid}$}}}\) on size_inp, where \(1 \leq i \leq m\). During this time 0 will be output on ready_out.
After inputting \(B_m\), the user keeps inputting 0 on skip_inp and move_inp until ready_out becomes 1. On the cycle when this happens the hash of \(key {{\mbox{$\|$}}}M\) will appear on digest_out. The number of cycles taken depends on \({{\mbox{${\mid}B_m{\mid}$}}}\). If \({{\mbox{${\mid}B_m{\mid}$}}} \neq r{-}1\) then ready_out will become 1 on the cycle after \(B_m\) is input. If \({{\mbox{${\mid}B_m{\mid}$}}}= r{-}1\) then ready_out will become 1 the cycle after the cycle after \(B_m\) is input.
The MITB state-machine is implemented using combinational logic and three blocks of registers as in the schematic diagram below. Each block of registers, REGISTER in the diagram, stores the number of bits shown on the output wire labels; their initial power-up values are shown in brackets (e.g. the leftmost register block stored the state, which is encoded using two bits and is initially in state Ready.
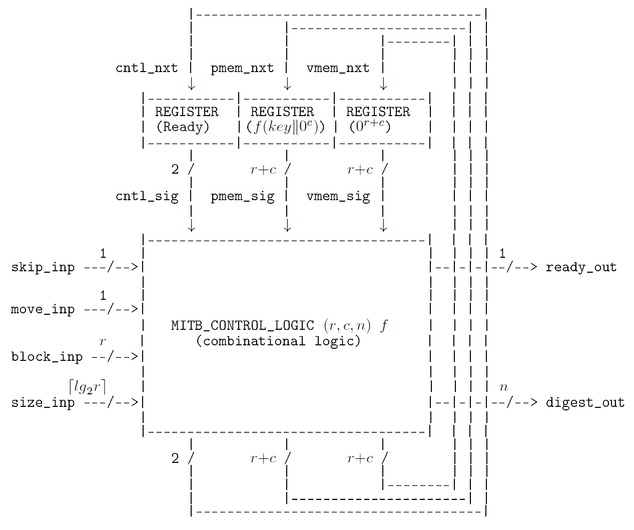
The block MITB_CONTROL_LOGIC is combinational logic and is parametrised on the permutation \(f\). This logic is specified in a HOL file as a Boolean function, which is unlikely to be interesting to readers of this document. Converting the Boolean function specification to a verified equivalent netlist of logic gates hasn’t been done, but would be straightforward, though a lot of work. The permutation \(f\) is defined in the Keccak documentation as a number of iterations (typically 24) of a function called a round, where each round is the function composition of five sub-round functions. Appendix A of the MITB report MITB.1.0 has more details. A realistic MITB implementation would probably use a sequential implementation of \(f\), perhaps with pipelining of the round/sub-round calculations, to minimise the number and depth of logic gates needed. Assuming \(f\) is implemented entirely in combinational logic, though perhaps unrealistic from an engineering perspective, seems reasonable for a first proof-of-concept exercise.
An MITB device is specified with a next-state function \({{\small\texttt{MITB}}}\) that gives the next state \(s'\) when input \(i\) is received in state \(s\). The observable outputs are determined by the current state, so the specification is a Moore machine. The next-state function \({{\small\texttt{MITB}}}\) is parametrised on the Keccak parameters \((r,c,n)\) and permutation function \(f\); it thus takes these as arguments, hence \(s'=~{{\small\texttt{MITB}}}~(r,c,n)~f~(s,i)\).
To verify by formal proof that the hardware design implementing the MITB state-machine functions as it is supposed to do – e.g. correctly hashes messages via the API protocol sketched above – the specified functionality must be formalised and shown to be correctly realised by the implementation. This has been done in two stages.
First, the combination of registers and combinational logic comprising the implementation is shown to have the behaviour of the state-machine. Second, this behaviour is proved to correspond to the hashing protocol specified in the API. A flavour of these formal specification and verifications follows: for full details see the MITB web pages.
The implementation is at the register transfer level (RTL), but with a complex block of combinational logic (MITB_CONTROL_LOGIC in the diagram) specified as a boolean function parametrised on the Keccak size parameters \(r\), \(c\), \(n\) and the permutation \(f\). Devices are represented as relations between the input and output signals. Signals are modelled as functions from time to values. Time corresponds to the number of clock cycles that have elapsed and is represented by a natural number. If \(\sigma\) is a function modelling a signal, then \(\sigma(t)\) is the value at the \(t^{\textrm{th}}\) clock cycle.
If \({{{\small\texttt{MITB}}}{\_}{{\small\texttt{IMP}}}}~(r,c,n)~f\) is the relation modelling the implementation with parameter values \((r,c,n)\) and \(f\), then \({{{\small\texttt{MITB}}}{\_}{{\small\texttt{IMP}}}}~(r,c,n)~f~(\sigma_{s},\sigma_{i},\sigma_{o})\) means that the signals \(\sigma_{s}\), \(\sigma_{i}\) and \(\sigma_{o}\) are in the \({{{\small\texttt{MITB}}}{\_}{{\small\texttt{IMP}}}}~(r,c,n)~f\) relation. The signals \(\sigma_{s}\), \(\sigma_{i}\) and \(\sigma_{o}\) represent the sequences of states, inputs and outputs on each clock cycle, respectively. They are are multi-bit wide: \(\sigma_{s}\) is the sequence of states (Ready or Absorbing, encoded using two bits), \(\sigma_{i}\) amalgamates inputs skip_inp, move_inp, block_inp and size_inp and \(\sigma_{o}\) amalgamates outputs ready_out and digest_out. The correctness of the implementation with respect to the next-state function \({{\small\texttt{MITB}}}\) is proved as a theorem which – ignoring some minor technical conditions – has the form:
\(\begin{array}{l} \vdash \forall \sigma_{s}~\sigma_{i}~\sigma_{o}.\\ \phantom{\vdash \forall}~{{{\small\texttt{MITB}}}{\_}{{\small\texttt{IMP}}}}~(r,c,n)~f~(\sigma_{s},\sigma_{i},\sigma_{o})\\ \phantom{\vdash \forall}\Leftrightarrow\\ \phantom{\vdash \forall}~ \forall t. \sigma_{s}(t{+}1)~{=}~{{\small\texttt{MITB}}}~(r,c,n)~f~(\sigma_{s}(t),\sigma_{i}(t)) \end{array}\)
Melham’s book gives an excellent description of the standard hardware modelling and verification techniques used to specify and verify MITB’s functional correctness. The details of how these techniques are utilised, including the actual theorems proved, can be found via the MITB web page.
A version of Linear Temporal Logic (LTL) is used to specify the API. Mathematical details of this logic are not given here, but are explained in the MITB Technical Report. A temporal formula \(\phi\) is a predicate on MITB executions: for each execution \(\sigma\), either \(\phi\) is true of \(\sigma\) or it is false of it. Five properties of the MITB API have been formalised: \({{\texttt{Init}}}\), \({{\texttt{Freeze}}}\), \({{\texttt{Reset}}}\), \({{\texttt{KeyUpdate}}}\), \({{\texttt{ComputeMAC}}}\).
\({{\texttt{Init}}}~key~c~f\) specifies that the ‘power up’ state of MITB is Ready, that zeros are being output on digest_out and that \(f(key{{\mbox{$\|$}}}{{\small\texttt{Zeros}}}(c))\) is stored in permanent memory (where \({{\small\texttt{Zeros}}}(c)\) is a string consisting of \(c\) 0s).
\({{\texttt{Freeze}}}\) specifies that the state and outputs of MITB remains unchanged as long as 1 is input on skip_inp.
\({{\texttt{Reset}}}\) specifies that inputting 1 on move_inp and 0 on skip_inp in an Absorbing state, i.e. when ready_out is 0, results in a return to the Ready state on the next cycle, with permanent memory unchanged and \({{\small\texttt{Zeros}}}~n\) being output at ready_out.
\({{\texttt{KeyUpdate}}}~r~c~f\) specifies that when in state Ready, inputting 0 on both skip_inp and move_inp and inputting \(key\) (where \({{\mbox{${\mid}key{\mid}$}}}=r\)) on block_inp, results in \(f(key{{\mbox{$\|$}}}{{\small\texttt{Zeros}}}(c))\) being stored in the permanent memory and then remaining in the Ready state on the next cycle.
\({{\texttt{ComputeMAC}}}~(r,c,n)~f\) specifies that if the user follows the correct protocol for inputting a message then its digest is computed using the Keccak HMAC algorithm. The user is required to split the message into blocks and then input them and their lengths. An individual block \(bk\) is input by putting it on block_inp and its size \({{\mbox{${\mid}bk{\mid}$}}}\) on size_inp whilst holding both skip_inp and move_inp at 0.
To give just an impression of how these properties are expressed in LTL, their definitions are given in the five boxes below. The contents of these boxes are not meant to be comprehensible as, amongst other things, they contain unexplained symbols. They are here to try to give a rough idea of API specification in LTL.
\(\small\begin{array}{|l|}\hline \\ {{\texttt{Init}}}~key~c~n~f~=\\ ~{{\small\textsf{readyOut}}}({{\small\texttt{T}}})~{{\small\texttt{And}}}~{{\small\textsf{digestOut}}}({{\small\texttt{Zeros}}}~n)~{{\small\texttt{And}}}~{{\small\textsf{pmemState}}}(f(key{{\mbox{$\|$}}}{{\small\texttt{Zeros}}}(c)))\\ {\phantom{++++++++++++++++++++++++++++++++++++.}}\\ \hline \end{array}\)
\(\small\begin{array}{|l|}\hline \\ {{\texttt{Freeze}}}~=\\ ~{{\small\texttt{Always}}}\\ ~~({{\small\texttt{Forall}}}~s~b_1~b_2\\ \phantom{~~(}~{{\small\textsf{skipInp}}}({{\small\texttt{T}}})~{{\small\texttt{And}}}~ {{\small\textsf{pmemState}}}(s)~{{\small\texttt{And}}}~{{\small\textsf{readyOut}}}(b_1)~{{\small\texttt{And}}}~{{\small\textsf{digestOut}}}(b_2)\\ \phantom{~~(}~{{\small\texttt{Implies}}}\\ \phantom{~~(}~{{\small\texttt{Next}}}({{\small\textsf{pmemState}}}(s)~{{\small\texttt{And}}}~{{\small\textsf{readyOut}}}(b_1)~{{\small\texttt{And}}}~{{\small\textsf{digestOut}}}(b_2)))\\ {\phantom{++++++++++++++++++++++++++++++++++++.}}\\ \hline \end{array}\)
\(\small\begin{array}{|l|}\hline \\ {{\texttt{Reset}}}~n~=\\ ~{{\small\texttt{Always}}}\\ ~~({{\small\texttt{Forall}}}~s.\\ \phantom{~~(}~({{\small\textsf{moveInp}}}({{\small\texttt{T}}})~{{\small\texttt{And}}}~{{\small\textsf{skipInp}}}({{\small\texttt{F}}})~{{\small\texttt{And}}}~{{\small\textsf{readyOut}}}({{\small\texttt{F}}})~{{\small\texttt{And}}}~{{\small\textsf{pmemState}}}(s))\\ \phantom{~~(}~{{\small\texttt{Implies}}}\\ \phantom{~~(}~{{\small\texttt{Next}}}({{\small\textsf{readyOut}}}({{\small\texttt{T}}})~{{\small\texttt{And}}}~{{\small\textsf{pmemState}}}(s)~{{\small\texttt{And}}}~{{\small\textsf{digestOut}}}({{\small\texttt{Zeros}}}~n)))\\ {\phantom{++++++++++++++++++++++++++++++++++++.}}\\ \hline \end{array}\)
\(\small\begin{array}{|l|}\hline \\ {{\texttt{KeyUpdate}}}~r~c~f~=\\ ~{{\small\texttt{Always}}}\\ ~~(({{\small\textsf{readyOut}}}({{\small\texttt{T}}})~{{\small\texttt{And}}}~{{\small\textsf{skipInp}}}({{\small\texttt{F}}})~{{\small\texttt{And}}}~{{\small\textsf{moveInp}}}({{\small\texttt{F}}}))\\ \phantom{~~(}{{\small\texttt{Implies}}}\\ \phantom{~~(}({{\small\texttt{Forall}}}~key.\\ \phantom{~~(}~~{{\small\textsf{blockInp}}}(key)~{{\small\texttt{And}}}~{{\small\texttt{Bool}}}({{\mbox{${\mid}key{\mid}$}}}=r)~\\ \phantom{~~(}~~{{\small\texttt{Implies}}}~{{\small\texttt{Next}}}({{\small\textsf{readyOut}}}({{\small\texttt{T}}})~{{\small\texttt{And}}}~{{\small\textsf{pmemState}}}(f(key {{\mbox{$\|$}}}{{\small\texttt{Zeros}}}(c))))))\\ {\phantom{++++++++++++++++++++++++++++++++++++.}}\\ \hline \end{array}\)
\(\small\begin{array}{|l|}\hline \\ {{\texttt{ComputeMAC}}}~(r,c,n)~f~=\\ ~{{\small\texttt{Always}}}\\ ~~({{\small\texttt{Forall}}}~\mathit{key}~m.\\ \phantom{~~(}~ ({{\small\textsf{readyOut}}}({{\small\texttt{T}}})~{{\small\texttt{And}}}~{{\small\textsf{skipInp}}}({{\small\texttt{F}}})~{{\small\texttt{And}}}~{{\small\textsf{moveInp}}}({{\small\texttt{T}}})\\ \phantom{~~((}~{{\small\texttt{And}}}~{{\small\texttt{Bool}}}({{\mbox{${\mid}\mathit{key}{\mid}$}}}=r)~{{\small\texttt{And}}}~{{\small\textsf{pmemState}}}(f(\mathit{key} {{\mbox{$\|$}}}{{\small\texttt{Zeros}}}(c))))\\ \phantom{~~(}~{{\small\texttt{Implies}}}\\ \phantom{~~(}~{{\small\texttt{Next}}}\\ ~~~~ ({{\small\texttt{InputBlocks}}}~r~({{\small\texttt{Split}}}~r~m)\\ ~~~\phantom{(}~ {{\small\texttt{Implies}}}\\ ~~~\phantom{(}~ ({{\small\textsf{readyOut}}}({{\small\texttt{F}}})~{{\small\texttt{And}}}~{{\small\textsf{digestOut}}}({{\small\texttt{Zeros}}}~n))\\ ~~~\phantom{(}~ {{\small\texttt{UntilN}}}(\texttt{if}~{{\mbox{${\mid}m{\mid}$}}}~{{\small\texttt{MOD}}}~r=r{-}1~ \texttt{then}~{{\mbox{${\mid}m{\mid}$}}}~{{\small\texttt{DIV}}}~r+2~\texttt{else}~{{\mbox{${\mid}m{\mid}$}}}~{{\small\texttt{DIV}}}~r+1)\\ ~~~\phantom{(}~ ({{\small\textsf{readyOut}}}({{\small\texttt{T}}})~\\ \phantom{(~~~(~}{{\small\texttt{And}}}~ {{\small\textsf{digestOut}}}({{\small\texttt{MAC}}}~\mathit{key}~(r,c,n)~m)\\ \phantom{(~~~(~}{{\small\texttt{And}}}~ {{\small\textsf{pmemState}}}(f(\mathit{key} {{\mbox{$\|$}}}{{\small\texttt{Zeros}}}(c))))))\\ {\phantom{++++++++++++++++++++++++++++++++++++.}}\\ \hline \end{array}\)
All of these properties have been shown to hold of all executions of the MITB implementation using the HOL4 proof assistant. The significance of this verification is discussed below.
I have a very limited understanding of security, so what I write here could range from naively superficial to completely wrong!
Verifying security is far more subtle and intricate than proving functional correctness. Even formulating what security means is contentious. There are at least three aspects of MITB’s security that could be analysed.
The operations in the API could be proved to be free of undesirable functionality, like allowing the secret key to be extracted.
The algorithms used to create an HMAC digest could be proved to be ‘cryptographically strong’, e.g. a brute force attack on a message digest will have low probability of finding the message in a feasible time.
The physical hardware implementing MITB could be shown not to be vulnerable to reverse engineering and also that it does not leak information through side channels such as the time taken to perform a hash or power usage fluctuations or electromagnetic radiation.
The third of these security aspects, physical attacks, is beyond the scope of the MITB project, thought we did discuss packaging the FPGA in simple tamper-resistant packaging. Two scary articles on the difficultly of achieving good physical security appeared whilst I was writing this:
Physical Key Extraction Attacks on PCs (June 2016 CACM)
This ‘Demonically Clever’ Backdoor Hides In a Tiny Slice of a Computer Chip (June 2016 Wired)
The academic paper A2: Analog Malicious Hardware behind the Wired article discusses ‘split manufacturing’ of chips:
The idea behind defences incorporating split manufacturing is to divide a chip into two parts, with one part being fabricated by a cheap, but untrusted, fabrication house, while the other part gets fabricated by an expensive, but trusted, fabrication house (that is also responsible for putting the two parts together …
The idea behind hardware tokens has similarities: splitting off functionality that needs to be trusted – password hashing in the case of MITB – into a separate device that could be designed, verified and made by a specialist high integrity manufacturer. Even if MITB could be made extremely trustworthy, there is still the problem of ensuring that the total system in which it is used – e.g. an MITB USB stick plugged into an off-the-shelf PC – actually benefits from the trustworthiness. The problem of putting together the parts of a split manufactured chips is also discussed in the A2 paper.
The CACM paper ends with:
How can we formally model the feasible side-channel attacks on PCs? What engineering methods will ensure devices comply with the model? And what algorithms, when running on compliant devices, will provably protect their secrets, even in the presence of side-channel attacks?
The next two sections outline work done on verifying the first and second aspects of MITB’s security: API functionality and computational cryptographic strength. The third aspect, physical security, is not considered further.
The only functional security property that has verified to hold of the MITB model is to prove that in all reachable states, the value output at digest_out is either \({{\small\texttt{Zeros}}}~n\) or the hash of some message. This property was proposed by Robert and is called \({{\texttt{Secure}}}~(r,c,n)~f\) here; its definition is below. Like the other definitions of temporal properties given above, this is only here to convey an impression of the formalisation. Further explanation is in the MITB progress report.
\(\small\begin{array}{|l|}\hline \\ {{\texttt{Secure}}}~(r,c,n)~f~=\\ ~{{\small\texttt{Always}}}({{\small\textsf{digestOut}}}({{\small\texttt{Zeros}}}~n)~{{\small\texttt{Or}}}~{{\small\texttt{Exists}}}~m.~{{\small\textsf{digestOut}}}({{\small\texttt{Hash}}}~(r,c,n)~f~({{\small\texttt{Zeros}}}(r{+}c))~m))\\ {\phantom{++++++++++++++++++++++++++++++++++++.}}\\ \hline \end{array}\)
The proof that \({{\texttt{Secure}}}~(r,c,n)~f\) holds of all executions of MITB shows that no combination of sequences of inputs can cause the secret key to be extracted unless this key is the hash of some string. This was an early property suggested by Robert and, in fact, the first MITB design didn’t satisfy it. I’m not sure how strong a result this is, but it does seem at least to show that MITB is not susceptible to Tookan-like attacks.
The functional security discussed in the preceding section is similar to a Dolev-Yao analyses of protocols in that it assumes cryptographic primitives are modelled using abstract operators, namely the uninterpreted permutation function \(f\). An actual MITB device implements the Keccak HMAC algorithm with the actual permutation \(f\) specified as part of Keccak – see Appendix A starting on Page 20 of the MITB report. Both the designers of Keccak and others have obtained cryptanalysis results that, presumably, provide some confidence that Keccak is good.
Robert, as well as designing the MITB state-machine, has completed a proof of the security of the MITB protocol based on universal composability (UC). This proof formalises security as the indistinguishability of an ideal functionality from the MITB implementation. It says that assuming an invariant on the relation between the state of an MITB and the state of a functionality, the follow-up states have the same relation. This implies that their outputs are the same (theorem online here) and hence security follows because the functionality is secure by construction, when the hash function is substituted by a random oracle. Robert’s proof of the main theorem is online at https://github.com/CakeML/mitb; the main theorem starts here.
Although MITB is tiny and the verification very incomplete, it is hoped that it may have potential in provoking thoughts on combining traditional functional verification with more recent computational security analysis.
In the rest of this section what was done and wasn’t done is reviewed. Following that, there’s an attempt to consider some wider issues that might cast doubt on what has been achieved. Finally, possible future work is outlined.
The current specification has not been validated as a usable API description. Although some proofs have been done showing that the state-machine implements the API, the list of properties proved is ad hoc. Whilst they are consistent, since the MITB implementation is a model, how can one know if they are adequate?
There is no evidence that the communication model used to relate MITB and its ideal functionality specification is really a good formalisation of UC. However, the proof is complete and there is unpublished work by others using EasyCrypt based on a very similar communication model that gives some evidence that the approach can provide simple composition. This give some confidence in the methodology.
Some of the MITB verification proofs are verbose and clumsy, and unlikely to be comprehensible by anyone besides their authors.
The API operations of MITB are ad hoc: the effects of the various inputs may well be badly designed. For example, having the stored key reset whenever move_inp is 0 in the Ready state may be dangerous: an attacker could surreptitiously reset the key. Adjusting the API would be easy (e.g. by just removing the ability to reset the key).
There are two major omissions in the work so far. The first major omission is that the MITB design is not realistic hardware. The input block_inp is 1600-bits wide and the input size_inp is a number. Whilst the latter is trivial to fix by encoding the numbers as bitstrings, the former will require sequential buffering, say to accumulate blocks 16-bits at a time over a 100 cycles. Adapting the state machine to do this should be straightforward, and the temporal logic specifications should be easy to adapt to work with the additional data acquisition cycles, and most of the existing proofs should be reusable. The work involved is classical data and temporal abstraction (see Melham’s book), but this is all work which has not been done.
The second major omission is that the multi-round \(f\) permutation function has not been implemented. It is treated in a Dolev-Yao style as an uninterpreted function. This nicely separates the API aspects of MITB from the cryptographic computation concerns, but a complete implementation would need hardware implementing \(f\), which might need several cycles (e.g. one for each sub-round), so also requiring temporal refinement as discussed in the previous paragraph. There is a discussion in Chapter 4 (Hardware) of the Keccak implementation overview. Although the \(f\) is quite complicated, creating a verified hardware designs implementing it should be straightforward (though possibly a lot of work due to all the intricate details). An approach using verifying synthesis might be appropriate.
Imagine the MITB design and verification have been completed, say down to synthesisable RTL represented in logic, but resembling a standard HDL like Verilog. What would have been achieved? All that would have been shown is that the API functionality specified in LTL is realised by the HDL model. Here are some worries that need to be assessed.
Cohn give an early discussion of issues related to some of those above that provoked a controversy – see Donald Mackenzie’s book Mechanizing Proof.
Finally, although MITB was conceived as part of a secure password secrecy system, it has not been discussed how such a complete system would work, so there is no analysis of what actual contribution to security an MITB device might make.
Completing the design and implementation would seem to be the essential first next step, but maybe it would be better to step back now and decide where the MITB project is going and what is most critical from a total system security perspective.
Careful thinking is needed to evaluate what contribution a formal verification of MITB could make to enhancing the security of using hashing in a real world setting.
The two pictures below are from an article published in 2017 in deepchip.com, an Electronic Design Automation (EDA) news and gossip website. It is predicted by Wally Rhines, the CEO of Mentor Graphics, a leading EDA company, that
“Chip designers will need to be concerned with malicious logic inside chips, counterfeit chips, and ‘side-channel’ attacks. Verification’s traditional focus has been verifying that a chip does what it is supposed to do. The new challenge is to verify that a chip does nothing it is not supposed to do. Wally thinks EDA will be the core of this solution.”


This opinion from the EDA industry supports what was said in the Introduction: I think the goals of the MITB project are still timely and scientifically challenging, so I hope the project might someday be revived.
First complete draft: May 25, 2016.