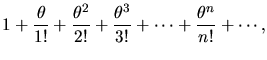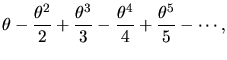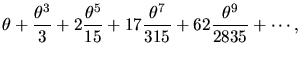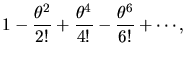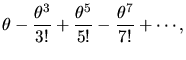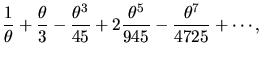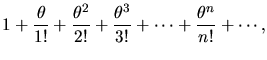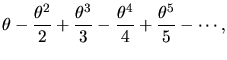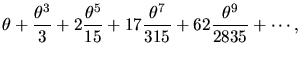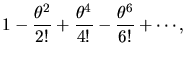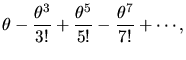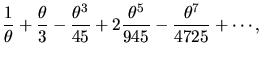Next: Expansions and Basis Functions
Up: No Title
Previous: Analysis: Real- and Complex-Valued
Imagine that you are an 18th-Century astronomer, hard at work on
Celestial Mechanics.
Understanding and predicting planetary motions requires calculating huge
numbers of trigonometric functions such as sine and cosine. Obviously,
this is before the age of computers or calculators, or mathematical tables.
How would you compute the sine, the cosine, or the tangent ...,
of some angle???
(How did they do it??)
Functions such as sine, cosine, logarithm, exponential, hyperbolic cotangent,
and so forth, are called transcendental functions. They are defined
in terms of the limits of power series: infinite series of terms
involving the argument of the function (the argument of f(x) is x;
the argument of
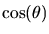 is
is
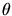 ), raised to an integer power, with
associated coefficients in front. Here are some examples of power series
that define transcendental functions:
), raised to an integer power, with
associated coefficients in front. Here are some examples of power series
that define transcendental functions:
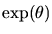 |
= |
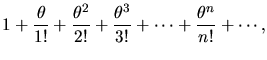 |
(1) |
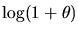 |
= |
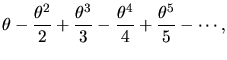 |
(2) |
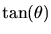 |
= |
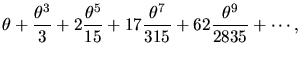 |
(3) |
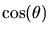 |
= |
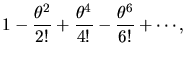 |
(4) |
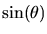 |
= |
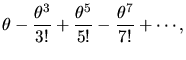 |
(5) |
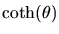 |
= |
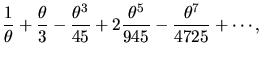 |
(6) |
Such expressions - truncated after a certain number of terms - are
precisely how computers and calculators evaluate these functions. There
is no other way to do it! That is why, if you were the Principal Assistant
to the Astronomer Royal in 1720, you spent all of your time with ink quill
and paper calculating endless power series such as the above.... :-(



Next: Expansions and Basis Functions
Up: No Title
Previous: Analysis: Real- and Complex-Valued
Neil Dodgson
2000-10-23