


Next: Power Series and Transcendental
Up: No Title
Previous: Purposes of this Course
Functions are mappings from some domain to some range. The domain might be
the real line (denoted
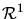 ), such as time, or the real plane
(denoted
), such as time, or the real plane
(denoted
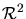 ), such as an optical image. The range refers to
the mapped value or values associated with all the points in the domain.
For example, the function might associate to each point on the line or the
plane just another real value (a scalar, such as temperature),
or an ordered set of real
values (a vector). A weather map showing wind velocity at each
point in Britain exemplifies a vector-valued function of the real plane;
and so on.
), such as an optical image. The range refers to
the mapped value or values associated with all the points in the domain.
For example, the function might associate to each point on the line or the
plane just another real value (a scalar, such as temperature),
or an ordered set of real
values (a vector). A weather map showing wind velocity at each
point in Britain exemplifies a vector-valued function of the real plane;
and so on.
Functions may also associate a complex-valued quantity to each point in
the domain. Complex variables are denoted
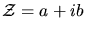 where
where
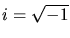 , and
a is the real part and b is the imaginary part of
, and
a is the real part and b is the imaginary part of 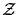 .
For example, the Fourier Transform of a musical melody associates a complex
variable to every possible frequency, each of which is represented by a
point in the (real-valued) frequency domain.
.
For example, the Fourier Transform of a musical melody associates a complex
variable to every possible frequency, each of which is represented by a
point in the (real-valued) frequency domain.
The complex conjugate of 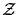 is denoted by the asterisk (*),
and it simply requires changing the sign of the imaginary part. Thus, the
complex conjugate of
is denoted by the asterisk (*),
and it simply requires changing the sign of the imaginary part. Thus, the
complex conjugate of
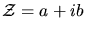 is:
is:
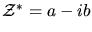 .
.
The modulus of a complex variable
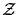 is
is
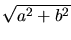 and it is denoted by
and it is denoted by
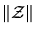 . It is easy to see that
. It is easy to see that
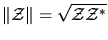 .
.
The angle of a complex variable
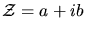 is
is
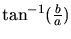 and it is denoted
and it is denoted
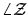 .
.
A very important
relation that we will use
later is:
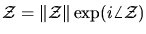 .
This can be regarded simply as converting the complex variable
.
This can be regarded simply as converting the complex variable 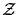 from its ``Cartesian" form a + i b (where the real part a and the
imaginary part b form orthogonal axes defining the complex plane), to
polar form
from its ``Cartesian" form a + i b (where the real part a and the
imaginary part b form orthogonal axes defining the complex plane), to
polar form
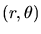 in which r is the modulus, or length
in which r is the modulus, or length
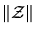 of the complex variable, and
of the complex variable, and 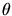 is its
angle
is its
angle
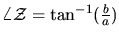 .
.
These relations and constructions are central to Fourier analysis and
harmonic analysis, which in turn are the mathematical cornerstone of
all of electrical engineering involving linear devices; optics;
holography; broadcast communications; electronic filter theory; acoustics;
quantum mechanics;
wave phenomena; much of mechanical engineering, and most of physics!
Indeed, the great Nobel Laureate in Physics, Julian Schwinger, once
said: ``There are only two problems that we can solve in Physics.
One is the simple harmonic oscillator [described in terms of the above
complex variables]; and
the second problem reduces to that one."



Next: Power Series and Transcendental
Up: No Title
Previous: Purposes of this Course
Neil Dodgson
2000-10-23