


Next: Orthogonality, Orthonormality, Inner Products,
Up: No Title
Previous: Power Series and Transcendental
The above power series express a function such as 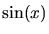 in terms of
an infinite series of power functions (like Axn) all added together.
More generally, almost any function f(x)can be represented perfectly as a linear combination of many other
types of functions besides power functions:
in terms of
an infinite series of power functions (like Axn) all added together.
More generally, almost any function f(x)can be represented perfectly as a linear combination of many other
types of functions besides power functions:
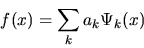 |
(7) |
where the chosen
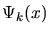 are called expansion basis functions.
For example, in the case of Fourier expansions in one dimension, the
expansion basis functions are the complex exponentials:
are called expansion basis functions.
For example, in the case of Fourier expansions in one dimension, the
expansion basis functions are the complex exponentials:
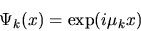 |
(8) |
``Finding the representation of some function in a chosen basis" means finding
the set of coefficients ak which, when multiplied by their
corresponding basis functions
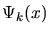 and the resulting linear
combination of basis functions are summed together, will exactly reproduce
the original function f(x) as per Eqt. (8).
and the resulting linear
combination of basis functions are summed together, will exactly reproduce
the original function f(x) as per Eqt. (8).
This is a very powerful tool, because it allows one to choose some universal
set of functions in terms of which all other (well-behaved) functions can
be represented just as a set of coefficients! In the case of systems
analysis, a major benefit of doing this is that
knowledge about how members of the chosen universal set of basis functions
behave in the system gives one omniscient knowledge about how any
possible input function will be treated by the system.



Next: Orthogonality, Orthonormality, Inner Products,
Up: No Title
Previous: Power Series and Transcendental
Neil Dodgson
2000-10-23
![]() in terms of
an infinite series of power functions (like Axn) all added together.
More generally, almost any function f(x)can be represented perfectly as a linear combination of many other
types of functions besides power functions:
in terms of
an infinite series of power functions (like Axn) all added together.
More generally, almost any function f(x)can be represented perfectly as a linear combination of many other
types of functions besides power functions: