Computer Laboratory – Course material 2009

Next: Computer Graphics and Image Up: Lent Term 2010: Part Previous: Compiler Construction Contents

Computation Theory

Lecturer: Professor A.M. Pitts

No. of lectures: 12

Prerequisite course: Discrete Mathematics

This course is a prerequisite for Complexity Theory (Part IB), Quantum Computing (Part II).

Aims

The aim of this course is to introduce several apparently different formalisations of the informal notion of algorithm; to show that they are equivalent; and to use them to demonstrate that there are uncomputable functions and algorithmically undecidable problems.

Lectures

Introduction: algorithmically undecidable problems. Decision problems. The informal notion of algorithm, or effective procedure. Examples of algorithmically undecidable problems. [1 lecture]
Register machines. Definition and examples; graphical notation. Register machine computable functions. Doing arithmetic with register machines. [1 lecture]
Universal register machine. Natural number encoding of pairs and lists. Coding register machine programs as numbers. Specification and implementation of a universal register machine. [2 lectures]
Undecidability of the halting problem. Statement and proof. Example of an uncomputable partial function. Decidable sets of numbers; examples of undecidable sets of numbers. [1 lecture]
Turing machines. Informal description. Definition and examples. Turing computable functions. Equivalence of register machine computability and Turing computability. The Church-Turing Thesis. [2 lectures]
Primitive and partial recursive functions. Definition and examples. Existence of a recursive, but not primitive recursive function. A partial function is partial recursive if and only if it is computable. [2 lectures]
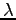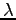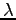$\lambda$ -Calculus. Alpha and beta conversion. Normalization. Encoding data. Writing recursive functions in the $\lambda$ -calculus. The relationship between computable functions and $\lambda$ -definable functions. [3 lectures]

Objectives

At the end of the course students should

be familiar with the register machine, Turing machine and 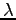$\lambda$ -calculus models of computability;
understand the notion of coding programs as data, and of a universal machine;
be able to use diagonalisation to prove the undecidability of the Halting Problem;
understand the mathematical notion of partial recursive function and its relationship to computability.

Recommended reading

* Hopcroft, J.E., Motwani, R. & Ullman, J.D. (2001). Introduction to automata theory, languages, and computation. Addison-Wesley (2nd ed.).
* Hindley, J.R. & Seldin, J.P. (2008). Lambda-calculus and combinators, an introduction. Cambridge University Press (2nd ed.).
Cutland, N.J. (1980). Computability: an introduction to recursive function theory. Cambridge University Press.
Davis, M.D., Sigal, R. & Weyuker, E.J. (1994). Computability, complexity and languages. Academic Press (2nd ed.).
Sudkamp, T.A. (2005). Languages and machines. Addison-Wesley (3rd ed.).

Next: Computer Graphics and Image Up: Lent Term 2010: Part Previous: Compiler Construction Contents