Connect++ 0.6.0
A fast, readable connection prover for first-order logic.
Loading...
Searching...
No Matches
Public Member Functions | Private Member Functions | Private Attributes | Static Private Attributes | Friends | List of all members
StackProver Class Reference

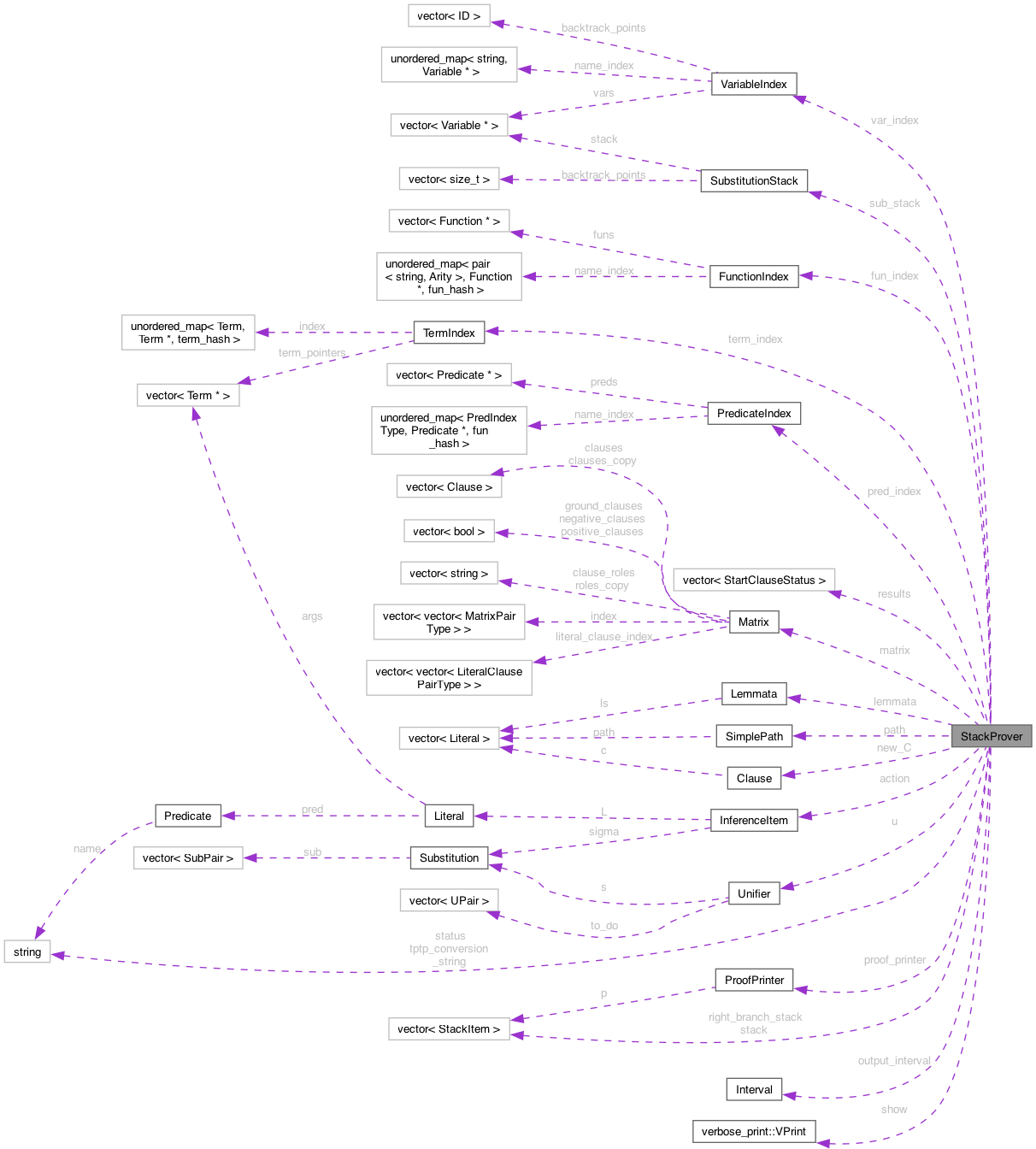
Prover using a pair of stacks to conduct the proof search. More...

#include <StackProver.hpp>

Collaboration diagram for StackProver:
Collaboration graph
[legend]

Public Member Functions

 StackProver ()
 You only need a basic constructor.
 
 StackProver (const StackProver &)=delete
 Don't try to copy this.
 
 StackProver (const StackProver &&)=delete
 
StackProver & operator= (const StackProver &)=delete
 
StackProver & operator= (const StackProver &&)=delete
 
std::tuple< VariableIndex *, FunctionIndex *, PredicateIndex *, TermIndex * > get_indexes ()
 Straightforward get method.
 
string get_status () const
 Straightforward get method.
 
void set_timeout (chrono::steady_clock::time_point time)
 Set a timeout.
 
void set_problem_path (fs::path &p)
 Set the path for the problem being solved.
 
void set_num_preds (size_t)
 Set the number of predicates.
 
void read_from_tptp_file (const string &, bool &, size_t &)
 Obviously, reads a problem from a TPTP file.
 
void add_equality_axioms (Predicate *)
 After reading a problem in which = and/or != appears, add the axioms for equality.
 
void deterministic_reorder (uint32_t n)
 Deterministically reorder the matrix n times.
 
void random_reorder ()
 Randomly reorder the matrix.
 
void random_reorder_literals ()
 Randomly reorder the literals in each clause in the matrix.
 
void show_matrix ()
 Show a nicely formatted matrix.
 
Matrix & get_matrix ()
 Get a reference to the matrix.
 
bool problem_is_cnf_only () const
 Find out whether the problem is CNF only.
 
bool problem_has_true_conjecture () const
 Find out whether the problem's conjecture
is $true.
 
bool problem_has_false_conjecture () const
 Find out whether the problem's conjecture
is $false.
 
bool problem_has_missing_conjecture () const
 Find out whether the problem's conjecture
is missing, in the sense that it didn't appear in the input file.
 
bool problem_has_negated_conjecture_removed () const
 Find out whether the problem's
negated conjecture was simplified out.
 
bool problem_has_fof_axioms () const
 Find out from the parser whether the problem had axioms before simplification.
 
bool simplified_problem_has_fof_axioms () const
 Find out from the parser whether the problem had axioms after simplification.
 
string get_tptp_conversion_string () const
 
void show_tptp_proof ()
 Show a Prolog-formatted proof.
 
ProverOutcome prove ()
 Here is where the magic happens.
 
vector< pair< string, vector< size_t > > > get_internal_proof () const
 Get an internal representation of the proof stack.
 
void show_statistics () const
 Display counts of number of extensions tried and so on.
 
void show_full_statistics (size_t) const
 Display counts of number of extensions tried and so on, as well as numbers per second.
 
void show_matrix () const
 
void show_path () const
 
void show_stack ()
 
void show_right_stack ()
 
void show_term_index ()
 

Private Member Functions

ProverResult go ()
 This runs the proof search from a given Start Move.
 
void populate_stack_item ()
 Fill the vector of possible actions with everything available.
 
void extend_with_action ()
 Take a single inference (action) and update the stacks accordingly.
 
bool depth_limited ()
 Test for the depth limit.
 
bool axiom () const
 Test to see if you're at an axiom.
 
void process_axiom_forward ()
 Start a right branch to continue from an axiom.
 
void backtrack_once ()
 Basic, single step backtrack on the stack.
 
void reduction_backtrack ()
 One of several different kinds of backtracking.
 
void lemmata_backtrack ()
 One of several different kinds of backtracking.
 
void left_extension_backtrack ()
 One of several different kinds of backtracking.
 
void right_extension_backtrack ()
 One of several different kinds of backtracking.
 
void set_up_start_clauses ()
 The start clauses to use depend on the settings, and the settings can change.
 
void reset_for_start ()
 Reset everything so that you can start from a specified start clause.
 

Private Attributes

size_t num_preds
 How many prdicates does the problem of interest have?
 
VariableIndex var_index
 This class needs one of each kind of index to keep track of Variables, Terms etc.
 
FunctionIndex fun_index
 This class needs one of each kind of index to keep track of Variables, Terms etc.
 
TermIndex term_index
 This class needs one of each kind of index to keep track of Variables, Terms etc.
 
PredicateIndex pred_index
 This class needs one of each kind of index to keep track of Variables, Terms etc.
 
SubstitutionStack sub_stack
 There is a separate stack to make application and removal of substitutions straightforward.
 
vector< StartClauseStatus > results
 This is populated by the StackProver::set_up_start_clauses method.
 
Matrix matrix
 A copy of the matrix you're working with.
 
SimplePath path
 At any point in the search process this is a copy of the path for the current node in the proof being constructed.
 
Clause new_C
 At any point in the search process this is a copy of the clause for the current node in the proof being constructed.
 
Lemmata lemmata
 At any point in the search process this is a copy of the list of lemmas for the current node in the proof being constructed.
 
Unifier u
 We need a single Unifier to use throughout the process.
 
InferenceItem action
 Stores the next action from the current StackItem.
 
size_t si
 Index of the current StackItem.
 
uint32_t current_depth_limit
 Self-explanatary.
 
uint32_t current_depth
 Self-explanatary.
 
bool depth_limit_reached
 Self-explanatary.
 
string status
 Problem status, if found in input file.
 
string tptp_conversion_string
 TPTP-friendly description of the clause conversion.
 
vector< StackItem > stack
 Main stack: this is constructed by the search process and, if completed, represents a proof.
 
vector< StackItem > right_branch_stack
 We build the proof by trying the left branches of extensions first: this stack keeps track of the right branches that we need to come back to.
 
bool backtrack
 Are we moving up or down the stack?
 
ProofPrinter proof_printer
 You need one of these to print LaTeX output or any kind of proof certificate.
 
fs::path problem_path
 Path for the problem of interest.
 
Interval output_interval
 How often do you output updates about progress?
 
uint32_t proof_count
 If we're searching for multiple proofs, keep count
of which one this is.
 
bool use_timeout
 Are we using a timeout?
 
chrono::steady_clock::time_point end_time
 When do we stop because of a timeout?
 
verbose_print::VPrint show
 Set up printing according to verbosity.
 
bool cnf_only
 Keep track of whether there were any FOF formulas in the problem file.
 
bool conjecture_true
 Keep track of whether the parser found the conjecture to be true.
 
bool conjecture_false
 Keep track of whether the parser found the conjecture to be false.
 
bool conjecture_missing
 Keep track of whether the parser found a conjecture in the problem file.
 
bool negated_conjecture_removed
 Keep track of whether the parser simplified the conjecture away.
 
bool fof_has_axioms
 Keep track of whether the parser found that it's an FOF problem with axioms before simplification.
 
bool simplified_fof_has_axioms
 Keep track of whether the parser found that it's an FOF problem with axioms after simplification.
 

Static Private Attributes

static uint32_t reductions_tried = 0
 We'll be keeping some simple statistics about the search process.
 
static uint32_t extensions_tried = 0
 We'll be keeping some simple statistics about the search process.
 
static uint32_t lemmata_tried = 0
 We'll be keeping some simple statistics about the search process.
 
static uint32_t right_branches_started = 0
 We'll be keeping some simple statistics about the search process.
 

Friends

ostream & operator<< (ostream &, const StackProver &)
 

Detailed Description

Prover using a pair of stacks to conduct the proof search.

This version is a straightforward translation of the proof method to search for a tree with all its leaves being axioms. However, by not using recursion we retain the ability to fully control backtracking and therefore, amongst other things, find all possible proofs.

This is really the main class for Connect++, and everything else essentially exists to support it. There's a lot going on here so hang on to your hat!

This is also one of only a small number of places where you'll need to modify stuff to incorporate machine learning. The main advice is simple: take notice of the comments that point out where to do this, and be very careful to leave the general stack manipulation code alone unless you really know what you're doing, because that stuff is quite easy to break.

Definition at line 74 of file StackProver.hpp.

Constructor & Destructor Documentation

◆ StackProver()

StackProver::StackProver ( )

You only need a basic constructor.

Definition at line 33 of file StackProver.cpp.

34: num_preds(0)
35, var_index()
36, fun_index()
37, term_index()
38, pred_index()
39, sub_stack()
40, results()
41, matrix()
42, path()
43, new_C()
44, lemmata()
45, u()
46, action(InferenceItemType::Start)
47, si(0)
48, current_depth_limit(0)
49, current_depth(1)
50, depth_limit_reached(false)
51, status()
52, tptp_conversion_string()
53, stack()
54, right_branch_stack()
55, backtrack(false)
56, proof_printer(&stack)
57, problem_path()
58, output_interval(params::output_frequency)
59, proof_count(0)
60, use_timeout(false)
61, end_time()
62, show(params::verbosity)
63, cnf_only(false)
64, conjecture_true(false)
65, conjecture_false(false)
66, conjecture_missing(false)
67, negated_conjecture_removed(false)
68, fof_has_axioms(false)
69, simplified_fof_has_axioms(false)
70{}
StackProver::depth_limit_reached
bool depth_limit_reached
Self-explanatary.
Definition StackProver.hpp:162
StackProver::status
string status
Problem status, if found in input file.
Definition StackProver.hpp:166
StackProver::results
vector< StartClauseStatus > results
This is populated by the StackProver::set_up_start_clauses method.
Definition StackProver.hpp:116
StackProver::negated_conjecture_removed
bool negated_conjecture_removed
Keep track of whether the parser simplified the conjecture away.
Definition StackProver.hpp:337
StackProver::current_depth_limit
uint32_t current_depth_limit
Self-explanatary.
Definition StackProver.hpp:154
StackProver::action
InferenceItem action
Stores the next action from the current StackItem.
Definition StackProver.hpp:146
StackProver::num_preds
size_t num_preds
How many prdicates does the problem of interest have?
Definition StackProver.hpp:80
StackProver::fof_has_axioms
bool fof_has_axioms
Keep track of whether the parser found that it's an FOF problem with axioms before simplification.
Definition StackProver.hpp:342
StackProver::stack
vector< StackItem > stack
Main stack: this is constructed by the search process and, if completed, represents a proof.
Definition StackProver.hpp:175
StackProver::matrix
Matrix matrix
A copy of the matrix you're working with.
Definition StackProver.hpp:120
StackProver::pred_index
PredicateIndex pred_index
This class needs one of each kind of index to keep track of Variables, Terms etc.
Definition StackProver.hpp:100
StackProver::right_branch_stack
vector< StackItem > right_branch_stack
We build the proof by trying the left branches of extensions first: this stack keeps track of the rig...
Definition StackProver.hpp:181
StackProver::proof_printer
ProofPrinter proof_printer
You need one of these to print LaTeX output or any kind of proof certificate.
Definition StackProver.hpp:190
StackProver::cnf_only
bool cnf_only
Keep track of whether there were any FOF formulas in the problem file.
Definition StackProver.hpp:321
StackProver::path
SimplePath path
At any point in the search process this is a copy of the path for the current node in the proof being...
Definition StackProver.hpp:126
StackProver::fun_index
FunctionIndex fun_index
This class needs one of each kind of index to keep track of Variables, Terms etc.
Definition StackProver.hpp:90
StackProver::lemmata
Lemmata lemmata
At any point in the search process this is a copy of the list of lemmas for the current node in the p...
Definition StackProver.hpp:138
StackProver::current_depth
uint32_t current_depth
Self-explanatary.
Definition StackProver.hpp:158
StackProver::tptp_conversion_string
string tptp_conversion_string
TPTP-friendly description of the clause conversion.
Definition StackProver.hpp:170
StackProver::simplified_fof_has_axioms
bool simplified_fof_has_axioms
Keep track of whether the parser found that it's an FOF problem with axioms after simplification.
Definition StackProver.hpp:347
StackProver::conjecture_missing
bool conjecture_missing
Keep track of whether the parser found a conjecture in the problem file.
Definition StackProver.hpp:333
StackProver::term_index
TermIndex term_index
This class needs one of each kind of index to keep track of Variables, Terms etc.
Definition StackProver.hpp:95
StackProver::proof_count
uint32_t proof_count
If we're searching for multiple proofs, keep count of which one this is.
Definition StackProver.hpp:226
StackProver::conjecture_false
bool conjecture_false
Keep track of whether the parser found the conjecture to be false.
Definition StackProver.hpp:329
StackProver::var_index
VariableIndex var_index
This class needs one of each kind of index to keep track of Variables, Terms etc.
Definition StackProver.hpp:85
StackProver::si
size_t si
Index of the current StackItem.
Definition StackProver.hpp:150
StackProver::conjecture_true
bool conjecture_true
Keep track of whether the parser found the conjecture to be true.
Definition StackProver.hpp:325
StackProver::backtrack
bool backtrack
Are we moving up or down the stack?
Definition StackProver.hpp:185
StackProver::end_time
chrono::steady_clock::time_point end_time
When do we stop because of a timeout?
Definition StackProver.hpp:234
StackProver::new_C
Clause new_C
At any point in the search process this is a copy of the clause for the current node in the proof bei...
Definition StackProver.hpp:132
StackProver::problem_path
fs::path problem_path
Path for the problem of interest.
Definition StackProver.hpp:194
StackProver::use_timeout
bool use_timeout
Are we using a timeout?
Definition StackProver.hpp:230
StackProver::sub_stack
SubstitutionStack sub_stack
There is a separate stack to make application and removal of substitutions straightforward.
Definition StackProver.hpp:105
StackProver::show
verbose_print::VPrint show
Set up printing according to verbosity.
Definition StackProver.hpp:238
StackProver::u
Unifier u
We need a single Unifier to use throughout the process.
Definition StackProver.hpp:142
StackProver::output_interval
Interval output_interval
How often do you output updates about progress?
Definition StackProver.hpp:198

Member Function Documentation

◆ add_equality_axioms()

void StackProver::add_equality_axioms ( Predicate * equals_predicate)

After reading a problem in which = and/or != appears, add the axioms for equality.

Parameters
equals_predicatePointer to a Predicate representing equals. This will have been obtained as an output from parsing the input file.

Definition at line 127 of file StackProver.cpp.

127 {
128 /*
129 * Equality axioms as described in Handbook of Automated
130 * Reasoning, Volume 1, page 615.
131 */
132 Arity max_fun_arity = fun_index.find_maximum_arity();
133 Arity max_pred_arity = pred_index.find_maximum_arity();
134 /*
135 * You need at least three variables to describe these, and
136 * twice as many as the arity of the biggest predicate or
137 * function.
138 */
139 uint32_t max_arity = max_fun_arity;
140 if (max_pred_arity > max_arity)
141 max_arity = max_pred_arity;
142 if (max_arity < 3)
143 max_arity = 3;
144 vector<Term*> xs;
145 vector<Term*> ys;
146 string xvar("__eqx_");
147 string yvar("__eqy_");
148 for (size_t i = 0; i < max_arity; i++) {
149 Variable* xvarp = var_index.add_named_var(xvar + std::to_string(i));
150 Variable* yvarp = var_index.add_named_var(yvar + std::to_string(i));
151 xs.push_back(term_index.add_variable_term(xvarp));
152 ys.push_back(term_index.add_variable_term(yvarp));
153 }
154 /*
155 * How you construct these depends on which representation you're using.
156 * It's easy enough to show that the difference is only a case
157 * of swapping negations. See for example "Equality Preprocessing in
158 * Connection Calculi", Oliver and Otten.
159 */
160 bool pol = !params::positive_representation;
161 uint32_t n_added = 0;
162 /*
163 * Axiom for reflexivity.
164 */
165 vector<Term*> ref;
166 ref.push_back(xs[0]);
167 ref.push_back(xs[0]);
168 Literal reflexive(equals_predicate, ref, 2, pol);
169 Clause ref_c;
170 ref_c.add_lit(reflexive);
171 matrix.add_clause(ref_c, "equality");
172 n_added++;
173 /*
174 * Axiom for symmetry.
175 */
176 vector<Term*> xy;
177 xy.push_back(xs[0]);
178 xy.push_back(xs[1]);
179 vector<Term*> yx;
180 yx.push_back(xs[1]);
181 yx.push_back(xs[0]);
182 Literal sym1(equals_predicate, xy, 2, !pol);
183 Literal sym2(equals_predicate, yx, 2, pol);
184 Clause sym_c;
185 sym_c.add_lit(sym1);
186 sym_c.add_lit(sym2);
187 matrix.add_clause(sym_c, "equality");
188 n_added++;
189 /*
190 * Axiom for transitivity.
191 */
192 vector<Term*> yz;
193 yz.push_back(xs[1]);
194 yz.push_back(xs[2]);
195 vector<Term*> xz;
196 xz.push_back(xs[0]);
197 xz.push_back(xs[2]);
198 Literal tr1(equals_predicate, xy, 2, !pol);
199 Literal tr2(equals_predicate, yz, 2, !pol);
200 Literal tr3(equals_predicate, xz, 2, pol);
201 Clause tr_c;
202 tr_c.add_lit(tr1);
203 tr_c.add_lit(tr2);
204 tr_c.add_lit(tr3);
205 matrix.add_clause(tr_c, "equality");
206 n_added++;
207 /*
208 * Function substitution.
209 */
210 for (size_t j = 0; j < fun_index.get_size(); j++) {
211 Function* p = fun_index[j];
212 Arity ar = p->get_arity();
213 if (ar > 0) {
214 Clause c;
215 vector<Term*> x1xn;
216 vector<Term*> y1yn;
217 for (size_t i = 0; i < ar; i++) {
218 x1xn.push_back(xs[i]);
219 y1yn.push_back(ys[i]);
220 vector<Term*> xiyi;
221 xiyi.push_back(xs[i]);
222 xiyi.push_back(ys[i]);
223 Literal eq_lit(equals_predicate, xiyi, 2, !pol);
224 c.add_lit(eq_lit);
225 }
226 vector<Term*> t;
227 t.push_back(term_index.add_function_term(p, x1xn));
228 t.push_back(term_index.add_function_term(p, y1yn));
229 Literal f_lit(equals_predicate, t, 2, pol);
230 c.add_lit(f_lit);
231 matrix.add_clause(c, "equality");
232 n_added++;
233 }
234 }
235 /*
236 * Predicate substitution.
237 */
238 for (size_t j = 0; j < pred_index.get_num_preds(); j++) {
239 Predicate* p = pred_index[j];
240 Arity ar = p->get_arity();
241 if (ar > 0 && p != equals_predicate) {
242 Clause c;
243 vector<Term*> x1xn;
244 vector<Term*> y1yn;
245 for (size_t i = 0; i < ar; i++) {
246 x1xn.push_back(xs[i]);
247 y1yn.push_back(ys[i]);
248 vector<Term*> xiyi;
249 xiyi.push_back(xs[i]);
250 xiyi.push_back(ys[i]);
251 Literal eq_lit(equals_predicate, xiyi, 2, !pol);
252 c.add_lit(eq_lit);
253 }
254 Literal p_lit1(p, x1xn, ar, !pol);
255 Literal p_lit2(p, y1yn, ar, pol);
256 c.add_lit(p_lit1);
257 c.add_lit(p_lit2);
258 matrix.add_clause(c, "equality");
259 n_added++;
260 }
261 }
262 /*
263 * Distinct objects
264 */
265 Arity min_arity = fun_index.find_minimum_arity();
266 if (!params::no_distinct_objects && min_arity == 0) {
267 vector<Term*> all_distinct_constants;
268 vector<Term*> empty_args;
269 for (size_t i = 0; i < fun_index.get_size(); i++) {
270 Function* p = fun_index[i];
271 Arity ar = p->get_arity();
272 // Remember, you don't want to do this for Skolem constants.
273 string name = p->get_name();
274 string prefix = name.string::substr(0,params::unique_skolem_prefix.length());
275 bool is_skolem = (params::unique_skolem_prefix.string::compare(0, string::npos, prefix) == 0) &&
276 (params::unique_skolem_prefix.length() < name.length());
277 bool is_quoted = (name[0] == '\"' && name[name.size() - 1] == '\"');
278 if (ar == 0 &&
279 !is_skolem &&
280 (params::all_distinct_objects || is_quoted)) {
281 Term* t = term_index.add_function_term(p, empty_args);
282 all_distinct_constants.push_back(t);
283 }
284 }
285 size_t s = all_distinct_constants.size();
286 if (s > 1) {
287 for (size_t i = s - 1; i > 0; i--) {
288 for (size_t j = 0; j < i; j++) {
289 Clause c;
290 vector<Term*> args;
291 args.push_back(all_distinct_constants[i]);
292 args.push_back(all_distinct_constants[j]);
293 Literal eq_lit(equals_predicate, args, 2, !pol);
294 c.add_lit(eq_lit);
295 matrix.add_clause(c, "distinct_objects");
296 n_added++;
297 }
298 }
299 }
300 }
301 matrix.set_num_equals(n_added);
302}
Clause
Representation of clauses.
Definition Clause.hpp:52
Clause::add_lit
void add_lit(const Literal &)
Add a literal, making sure you don't duplicate.
Definition Clause.cpp:96
Function
Basic representation of functions.
Definition Function.hpp:54
Function::get_arity
Arity get_arity() const
Most basic access function.
Definition Function.hpp:88
Function::get_name
string get_name() const
Most basic access function.
Definition Function.hpp:84
FunctionIndex::find_minimum_arity
Arity find_minimum_arity() const
Find the smallest arity appearing for any Function in the index.
Definition FunctionIndex.cpp:81
FunctionIndex::get_size
size_t get_size() const
Self-explanatory.
Definition FunctionIndex.hpp:96
FunctionIndex::find_maximum_arity
Arity find_maximum_arity() const
Find the largest arity appearing for any Function in the index.
Definition FunctionIndex.cpp:71
Literal
Basic representation of literals, bundling together (pointers to) a Predicate, a collection of argume...
Definition Literal.hpp:50
Matrix::add_clause
void add_clause(Clause &, string="")
Add a Clause to the Matrix and update the index accordingly.
Definition Matrix.cpp:97
Matrix::set_num_equals
void set_num_equals(uint32_t n)
Straightforward set method.
Definition Matrix.hpp:297
Predicate
Basic representation of predicates: here just names, ids and arities.
Definition Predicate.hpp:51
Predicate::get_arity
Arity get_arity() const
Basic get method.
Definition Predicate.hpp:90
PredicateIndex::get_num_preds
size_t get_num_preds() const
Basic get method.
Definition PredicateIndex.hpp:92
PredicateIndex::find_maximum_arity
Arity find_maximum_arity() const
Find the largest arity appearing in the index.
Definition PredicateIndex.cpp:66
Term
General representation of terms.
Definition Term.hpp:62
TermIndex::add_function_term
Term * add_function_term(Function *, const vector< Term * > &)
Self-explanatory: add a Term containing a function to the index.
Definition TermIndex.cpp:56
TermIndex::add_variable_term
Term * add_variable_term(Variable *)
Self-explanatory: add a Term containing a variable to the index.
Definition TermIndex.cpp:41
Variable
Basic representation of variables.
Definition Variable.hpp:58
VariableIndex::add_named_var
Variable * add_named_var(const string &)
Add a variable with the specified name to the index.
Definition VariableIndex.cpp:44

◆ axiom()

bool StackProver::axiom ( ) const
private

Test to see if you're at an axiom.

Definition at line 340 of file StackProver.cpp.

340 {
341 return stack[si].c.empty();
342}

◆ backtrack_once()

void StackProver::backtrack_once ( )
private

Basic, single step backtrack on the stack.

Careful though: you need to treat the depth of the tree correctly if you want to keep track of it.

Definition at line 546 of file StackProver.cpp.

546 {
547 backtrack = true;
548 stack.pop_back();
549 si--;
550 current_depth = stack[si].depth;
551}

◆ depth_limited()

bool StackProver::depth_limited ( )
private

Test for the depth limit.

Definition at line 331 of file StackProver.cpp.

331 {
332 bool result = ((params::limit_by_tree_depth && (current_depth >= current_depth_limit))
333 ||
334 (!params::limit_by_tree_depth && (stack[si].p.length() >= current_depth_limit)));
335 if (result)
336 depth_limit_reached = true;
337 return result;
338}

◆ deterministic_reorder()

void StackProver::deterministic_reorder ( uint32_t n)
inline

Deterministically reorder the matrix n times.

Parameters
nNumber of times to reorder.

Definition at line 424 of file StackProver.hpp.

424 {
425 matrix.deterministic_reorder(n);
426 }
Matrix::deterministic_reorder
void deterministic_reorder(size_t)
Deterministic reorder of the clauses.
Definition Matrix.cpp:133

◆ extend_with_action()

void StackProver::extend_with_action ( )
private

Take a single inference (action) and update the stacks accordingly.

Definition at line 344 of file StackProver.cpp.

344 {
345 /*
346 * Add a new StackItem using the next action from the list stored
347 * in the StackItem currently in play. If necessary, also
348 * add something to right_branch_stack. Populate the new list of
349 * actions and update si.
350 */
351 action = stack[si].get_next_inference(matrix, u);
352 current_depth++;
353 /*
354 * Why are the scope rules for switch so odd???
355 */
356 Clause old_C;
357 Lemmata old_Lem;
358 Literal neg_lit;
359 UnificationOutcome outcome;
360 Substitution sig;
361 Literal ext_L;
362 switch (action.T) {
363 //----------------------------------------------------------------------
364 //----------------------------------------------------------------------
365 //----------------------------------------------------------------------
366 // Lemmas.
367 //----------------------------------------------------------------------
368 //----------------------------------------------------------------------
369 //----------------------------------------------------------------------
370 case InferenceItemType::Lemma:
371 lemmata_tried++;
372 /*
373 * If you are restricting backtracking for lemmas then
374 * at this point you can remove all alternatives.
375 */
376 if (params::limit_bt_lemmas)
377 stack[si].restrict_backtrack();
378 /*
379 * Work out the new state.
380 */
381 new_C = stack[si].c;
382 new_C.drop_literal(action.Lindex);
383 path = stack[si].p;
384 lemmata = stack[si].l;
385 /*
386 * Extend the stack.
387 */
388 stack.emplace_back(StackItemType::Lemmata, new_C, path,
389 lemmata, current_depth);
390 stack.back().set_this_action(action);
391 break;
392 //----------------------------------------------------------------------
393 //----------------------------------------------------------------------
394 //----------------------------------------------------------------------
395 // Reduction.
396 //----------------------------------------------------------------------
397 //----------------------------------------------------------------------
398 //----------------------------------------------------------------------
399 case InferenceItemType::Reduction:
400 reductions_tried++;
401 /*
402 * If you are restricting backtracking for reductions then
403 * at this point you can remove all alternatives.
404 */
405 if (params::limit_bt_reductions)
406 stack[si].restrict_backtrack();
407 /*
408 * Reductions have a substitution, so apply it and remember
409 * in case you need to undo it later.
410 */
411 action.sigma.apply();
412 sub_stack.push_all(action.sigma);
413 /*
414 * Work out the new state.
415 */
416 new_C = stack[si].c;
417 new_C.drop_literal(action.Lindex);
418 path = stack[si].p;
419 lemmata = stack[si].l;
420 lemmata.push_back(action.L);
421 /*
422 * Extend the stack.
423 */
424 stack.emplace_back(StackItemType::Reduction, new_C, path,
425 lemmata, action.sigma, current_depth);
426 stack.back().set_this_action(action);
427 break;
428 //----------------------------------------------------------------------
429 //----------------------------------------------------------------------
430 //----------------------------------------------------------------------
431 // Extension.
432 //----------------------------------------------------------------------
433 //----------------------------------------------------------------------
434 //----------------------------------------------------------------------
435 case InferenceItemType::Extension:
436 extensions_tried++;
437 /*
438 * You're going to generate new variables, so remember where to
439 * backtrack to.
440 */
441 var_index.add_backtrack_point();
442 /*
443 * This is an Extension, so you're going to add something to
444 * right_branch_stack.
445 */
446 path = stack[si].p;
447 old_C = stack[si].c;
448 old_C.drop_literal(action.Lindex);
449 old_Lem = stack[si].l;
450 old_Lem.push_back(action.L);
451 /*
452 * DON'T do populate_stack_item here! That can wait until you actually
453 * use the right branch. In fact it *has* to wait because we might
454 * apply substitutions that affect it.
455 */
456 right_branch_stack.emplace_back(StackItemType::RightBranch, old_C,
457 path, old_Lem, current_depth);
458 /*
459 * The right branch needs to know where to restrict backtracking.
460 */
461 right_branch_stack.back().set_bt_restriction_index(stack.size() - 1);
462 /*
463 * Now you can deal with the left branch.
464 */
465 matrix.get_literal_clause_pair(action.index_in_LC_index, action.index_to_LC, ext_L, new_C);
466 new_C.make_copy_with_new_vars(ext_L, new_C, var_index, term_index);
467 /*
468 * Extensions have a substitution, so apply it and remember
469 * in case you need to undo it later.
470 */
471 neg_lit = action.L;
472 neg_lit.invert();
473 outcome = u(neg_lit, ext_L);
474 sig = u.get_substitution();
475 u.backtrack();
476 sig.apply();
477 sub_stack.push_all(sig);
478 /*
479 * Work out the new state.
480 */
481 path.push(action.L);
482 lemmata = stack[si].l;
483 /*
484 * Extend the stack.
485 */
486 stack.emplace_back(StackItemType::LeftBranch, new_C, path,
487 lemmata, sig, current_depth);
488 stack.back().set_this_action(action);
489 break;
490 default:
491 cerr << "PANIC!!! You should only have a lemmata, reduction or an extension here!"
492 << endl;
493 break;
494 }
495 /*
496 * Finally, move si on and work out the next bunch of possible actions.
497 */
498 si++;
499 populate_stack_item();
500}
Clause::make_copy_with_new_vars
Clause make_copy_with_new_vars(VariableIndex &, TermIndex &) const
Make a copy of an entire clause, introducing new variables.
Definition Clause.cpp:107
Clause::drop_literal
void drop_literal(LitNum)
Get rid of the specified Literal.
Definition Clause.cpp:155
Lemmata
Representation of the lemma list.
Definition Lemmata.hpp:49
Lemmata::push_back
void push_back(const Literal &)
Self-explanatory.
Definition Lemmata.cpp:28
Matrix::get_literal_clause_pair
void get_literal_clause_pair(LitNum, size_t, Literal &, Clause &) const
Get a literal and clause from the index.
Definition Matrix.cpp:301
StackProver::lemmata_tried
static uint32_t lemmata_tried
We'll be keeping some simple statistics about the search process.
Definition StackProver.hpp:216
StackProver::populate_stack_item
void populate_stack_item()
Fill the vector of possible actions with everything available.
Definition StackProver.cpp:304
StackProver::extensions_tried
static uint32_t extensions_tried
We'll be keeping some simple statistics about the search process.
Definition StackProver.hpp:211
StackProver::reductions_tried
static uint32_t reductions_tried
We'll be keeping some simple statistics about the search process.
Definition StackProver.hpp:206
Substitution
General representation of a substitution.
Definition Substitution.hpp:57
Substitution::apply
void apply() const
Apply a substitution everywhere.
Definition Substitution.cpp:56
SubstitutionStack::push_all
void push_all(Substitution &)
Take all the substitutions provided and add the corresponding variables to the stack.
Definition SubstitutionStack.cpp:28
Unifier::backtrack
void backtrack()
Apply the backtracking process to the substitution that has been constructed.
Definition Unifier.cpp:195
Unifier::get_substitution
Substitution get_substitution() const
Trivial get methods for the result.
Definition Unifier.hpp:122
VariableIndex::add_backtrack_point
void add_backtrack_point()
Add a backtrack point.
Definition VariableIndex.cpp:125
InferenceItem::Lindex
LitNum Lindex
The index of the literal within the clause being used.
Definition InferenceItem.hpp:73
InferenceItem::sigma
Substitution sigma
A copy of the substitution that makes the rule applicable. This may or may not be reusable,...
Definition InferenceItem.hpp:89
InferenceItem::L
Literal L
The Literal that is used to make the inference.
Definition InferenceItem.hpp:69
InferenceItem::index_to_LC
size_t index_to_LC
Estensions are performance-critical. We store the index into the literal_clause_index,...
Definition InferenceItem.hpp:110
InferenceItem::index_in_LC_index
size_t index_in_LC_index
Estensions are performance-critical. We store the index into the literal_clause_index,...
Definition InferenceItem.hpp:104
InferenceItem::T
InferenceItemType T
What kind of inference is this?
Definition InferenceItem.hpp:65

◆ get_indexes()

std::tuple< VariableIndex *, FunctionIndex *, PredicateIndex *, TermIndex * > StackProver::get_indexes ( )
inline

Straightforward get method.

Definition at line 363 of file StackProver.hpp.

363 {
364 auto result = std::make_tuple(&var_index, &fun_index, &pred_index, &term_index);
365 return result;
366 }

◆ get_internal_proof()

vector< pair< string, vector< size_t > > > StackProver::get_internal_proof ( ) const

Get an internal representation of the proof stack.

Definition at line 1227 of file StackProver.cpp.

1227 {
1228 return proof_printer.make_internal();
1229}
ProofPrinter::make_internal
vector< pair< string, vector< size_t > > > make_internal() const
Make a simple data structure representing the proof stack.
Definition ProofPrinter.cpp:339

◆ get_matrix()

Matrix & StackProver::get_matrix ( )
inline

Get a reference to the matrix.

Definition at line 450 of file StackProver.hpp.

450 {
451 return matrix;
452 };

◆ get_status()

string StackProver::get_status ( ) const
inline

Straightforward get method.

Definition at line 370 of file StackProver.hpp.

370{ return status; }

◆ get_tptp_conversion_string()

string StackProver::get_tptp_conversion_string ( ) const
inline

Definition at line 503 of file StackProver.hpp.

503 {
504 return tptp_conversion_string;
505 }

◆ go()

ProverResult StackProver::go ( )
private

This runs the proof search from a given Start Move.

Definition at line 652 of file StackProver.cpp.

652 {
653 /*
654 * Having set up a single entry on the stack, containing a start
655 * state, search for a proof.
656 *
657 * Either you return by ending at the start state with nothing left
658 * to try, by finding a proof, by depth limiting or by timing out.
659 *
660 * The backtrack variable is important here - when true you are
661 * (surprise surprise) backtracking. So mostly each case in the
662 * following switch is divided according to whether you're going
663 * forward or backtracking.
664 */
665 while(true) {
666 /*
667 * Test for and deal with a timeout.
668 */
669 if (use_timeout && chrono::steady_clock::now() > end_time)
670 return ProverResult::TimeOut;
671 /*
672 * Say what's going on.
673 */
674 if (output_interval.tick() && params::verbosity >= 2) {
675 cout << cursor_symbols::Cursor::to_column(1);
676 cout << cursor_symbols::Cursor::erase_line(2);
677 cout << "Reductions: " << reductions_tried << " Extensions: " << extensions_tried;
678 cout << " Lemmata: " << lemmata_tried << " Right branches: " << right_branches_started;
679 cout << " Stack size: " << stack.size();
680 cout.flush();
681 }
682 /*
683 * si must point to the back of the stack at this point.
684 *
685 * Remember that extend_with_action will deal with this for you.
686 */
687 switch (stack[si].item_type) {
688 //----------------------------------------------------------------
689 //----------------------------------------------------------------
690 //----------------------------------------------------------------
691 // Deal with the start state. Essentially straightforward. Just
692 // deal with a completed search, otherwise work out the
693 // possibly actions and get on with it.
694 //----------------------------------------------------------------
695 //----------------------------------------------------------------
696 //----------------------------------------------------------------
697 case StackItemType::Start:
698 backtrack = false;
699 if (stack[si].no_more_inferences())
700 return ProverResult::OptionsExhausted;
701 else
702 extend_with_action();
703 break;
704 //----------------------------------------------------------------
705 //----------------------------------------------------------------
706 //----------------------------------------------------------------
707 // Lemmas. Again, mostly straightforward.
708 //----------------------------------------------------------------
709 //----------------------------------------------------------------
710 //----------------------------------------------------------------
711 case StackItemType::Lemmata:
712 /*
713 * Operation is essentially similar to the reduction case.
714 *
715 * First deal with moving forward.
716 */
717 if (!backtrack) {
718 if (axiom()) {
719 /*
720 * Either you've found a proof or you try a right branch.
721 */
722 if (right_branch_stack.empty())
723 return ProverResult::Valid;
724 else
725 process_axiom_forward();
726 }
727 /*
728 * Backtrack because of depth limiting.
729 */
730 else if (depth_limited() && params::depth_limit_all)
731 lemmata_backtrack();
732 /*
733 * Backtrack because there's nothing left to try.
734 */
735 else if (stack[si].no_more_inferences())
736 lemmata_backtrack();
737 /*
738 * There must be something left to try, so try it.
739 */
740 else
741 extend_with_action();
742 }
743 /*
744 * We are moving down the stack.
745 */
746 else {
747 /*
748 * If you're backtracking then you need to jump over axioms.
749 */
750 if (axiom())
751 lemmata_backtrack();
752 /*
753 * If you're not at an axiom then you can start going forward
754 * again.
755 */
756 else
757 backtrack = false;
758 }
759 break;
760 //----------------------------------------------------------------
761 //----------------------------------------------------------------
762 //----------------------------------------------------------------
763 // Reduction. Almost identical to Lemmas, but note the
764 // slightly different backtracking requirement to take account
765 // of undoing the substitution.
766 //----------------------------------------------------------------
767 //----------------------------------------------------------------
768 //----------------------------------------------------------------
769 case StackItemType::Reduction:
770 /*
771 * We are moving up the stack.
772 */
773 if (!backtrack) {
774 if (axiom()) {
775 /*
776 * Either you've found a proof or you try a right branch.
777 */
778 if (right_branch_stack.empty())
779 return ProverResult::Valid;
780 else
781 process_axiom_forward();
782 }
783 /*
784 * Backtrack because of depth limiting.
785 */
786 else if (depth_limited() && params::depth_limit_all)
787 reduction_backtrack();
788 /*
789 * Backtrack because there's nothing left to try.
790 */
791 else if (stack[si].no_more_inferences())
792 reduction_backtrack();
793 /*
794 * There must be something left to try, so try it.
795 */
796 else
797 extend_with_action();
798 }
799 /*
800 * We are moving down the stack.
801 */
802 else {
803 /*
804 * If you're backtracking then you need to jump over axioms.
805 */
806 if (axiom())
807 reduction_backtrack();
808 /*
809 * If you're not at an axiom then you can start going forward
810 * again.
811 */
812 else
813 backtrack = false;
814 }
815 break;
816 //----------------------------------------------------------------
817 //----------------------------------------------------------------
818 //----------------------------------------------------------------
819 // Left branch of Extension. Mostly similar to the Reduction
820 // and Lemma cases, but the backtrack is again different to
821 // take care of the new variables, the substitution, and the
822 // right_branch_stack.
823 //----------------------------------------------------------------
824 //----------------------------------------------------------------
825 //----------------------------------------------------------------
826 case StackItemType::LeftBranch:
827 /*
828 * Operation is essentially similar to the Reduction and
829 * Lemma cases. See those for corresponding comments.
830 */
831 if (!backtrack) {
832 if (axiom())
833 process_axiom_forward();
834 else if (depth_limited() && !matrix.is_ground(stack[si].this_action.C_2))
835 left_extension_backtrack();
836 else if (stack[si].no_more_inferences())
837 left_extension_backtrack();
838 else
839 extend_with_action();
840 }
841 /*
842 * We are moving down the stack.
843 */
844 else {
845 if (axiom())
846 left_extension_backtrack();
847 else
848 backtrack = false;
849 }
850 break;
851 //----------------------------------------------------------------
852 //----------------------------------------------------------------
853 //----------------------------------------------------------------
854 // Right branch of Extension. Mostly similar to the Reduction
855 // and Lemmata cases, but the backtrack is now much more
856 // delicate. See the documentation for right_extension_backtrack.
857 //----------------------------------------------------------------
858 //----------------------------------------------------------------
859 //----------------------------------------------------------------
860 case StackItemType::RightBranch:
861 /*
862 * Operation is essentially similar to the reduction case.
863 */
864 if (!backtrack) {
865 if (axiom()) {
866 if (right_branch_stack.empty())
867 return ProverResult::Valid;
868 else
869 process_axiom_forward();
870 }
871 else if (depth_limited())
872 right_extension_backtrack();
873 else if (stack[si].no_more_inferences())
874 right_extension_backtrack();
875 else
876 extend_with_action();
877 }
878 /*
879 * We are moving down the stack.
880 */
881 else {
882 if (axiom())
883 right_extension_backtrack();
884 else
885 backtrack = false;
886 }
887 break;
888 //----------------------------------------------------------------
889 default:
890 cerr << "Something is VERY WRONG!" << endl;
891 break;
892 }
893 }
894 return ProverResult::Error;
895}
Interval::tick
bool tick()
Definition Interval.hpp:52
Matrix::is_ground
bool is_ground(size_t i) const
Is a particular Clause ground?
Definition Matrix.hpp:285
StackProver::process_axiom_forward
void process_axiom_forward()
Start a right branch to continue from an axiom.
Definition StackProver.cpp:502
StackProver::lemmata_backtrack
void lemmata_backtrack()
One of several different kinds of backtracking.
Definition StackProver.cpp:558
StackProver::extend_with_action
void extend_with_action()
Take a single inference (action) and update the stacks accordingly.
Definition StackProver.cpp:344
StackProver::depth_limited
bool depth_limited()
Test for the depth limit.
Definition StackProver.cpp:331
StackProver::left_extension_backtrack
void left_extension_backtrack()
One of several different kinds of backtracking.
Definition StackProver.cpp:562
StackProver::right_branches_started
static uint32_t right_branches_started
We'll be keeping some simple statistics about the search process.
Definition StackProver.hpp:221
StackProver::right_extension_backtrack
void right_extension_backtrack()
One of several different kinds of backtracking.
Definition StackProver.cpp:590
StackProver::reduction_backtrack
void reduction_backtrack()
One of several different kinds of backtracking.
Definition StackProver.cpp:553
StackProver::axiom
bool axiom() const
Test to see if you're at an axiom.
Definition StackProver.cpp:340
cursor_symbols::Cursor::erase_line
static string erase_line(uint8_t n)
Definition cursor.hpp:158

◆ left_extension_backtrack()

void StackProver::left_extension_backtrack ( )
private

One of several different kinds of backtracking.

Definition at line 562 of file StackProver.cpp.

562 {
563 /*
564 * You're backtracking through a left branch, so you
565 * need to remember to get rid of the corresponding
566 * right branch as well.
567 */
568 right_branch_stack.pop_back();
569 var_index.backtrack();
570 sub_stack.backtrack();
571 backtrack_once();
572}
StackProver::backtrack_once
void backtrack_once()
Basic, single step backtrack on the stack.
Definition StackProver.cpp:546
SubstitutionStack::backtrack
void backtrack()
Remove variables from the stack, and remove substitutions as you go, as far back as the most recent b...
Definition SubstitutionStack.cpp:36
VariableIndex::backtrack
void backtrack()
Backtrack to the last marker.
Definition VariableIndex.cpp:134

◆ lemmata_backtrack()

void StackProver::lemmata_backtrack ( )
private

One of several different kinds of backtracking.

Definition at line 558 of file StackProver.cpp.

558 {
559 backtrack_once();
560}

◆ populate_stack_item()

void StackProver::populate_stack_item ( )
private

Fill the vector of possible actions with everything available.

Definition at line 304 of file StackProver.cpp.

304 {
305 /*
306 * Don't waste your time if the regularity test applies.
307 */
308 if (params::use_regularity_test && !path.test_for_regularity(new_C))
309 return;
310 /*
311 * Don't try to populate axioms.
312 */
313 if (new_C.size() == 0) {
314 return;
315 }
316 /*
317 * Extensions and reductions.
318 */
319 stack[si].initialize(matrix, u);
320 /*
321 * Lemmas
322 */
323 if (params::use_lemmata) {
324 if (params::limit_lemmata)
325 lemmata.find_initial_lemmata(stack[si].actions, new_C);
326 else
327 lemmata.find_all_lemmata(stack[si].actions, new_C);
328 }
329}
Clause::size
size_t size() const
Straightforward get method.
Definition Clause.hpp:78
Lemmata::find_initial_lemmata
void find_initial_lemmata(vector< InferenceItem > &, Clause &)
Find all lemmata that are applicable, but only for the initial Literal in a Clause.
Definition Lemmata.cpp:33
Lemmata::find_all_lemmata
void find_all_lemmata(vector< InferenceItem > &, Clause &)
Find all lemmata that are applicable, given a Clause.
Definition Lemmata.cpp:56

◆ problem_has_false_conjecture()

bool StackProver::problem_has_false_conjecture ( ) const
inline

Find out whether the problem's conjecture
is $false.

Definition at line 471 of file StackProver.hpp.

471 {
472 return conjecture_false;
473 }

◆ problem_has_fof_axioms()

bool StackProver::problem_has_fof_axioms ( ) const
inline

Find out from the parser whether the problem had axioms before simplification.

Definition at line 493 of file StackProver.hpp.

493 {
494 return fof_has_axioms;
495 }

◆ problem_has_missing_conjecture()

bool StackProver::problem_has_missing_conjecture ( ) const
inline

Find out whether the problem's conjecture
is missing, in the sense that it didn't appear in the input file.

Definition at line 479 of file StackProver.hpp.

479 {
480 return conjecture_missing;
481 }

◆ problem_has_negated_conjecture_removed()

bool StackProver::problem_has_negated_conjecture_removed ( ) const
inline

Find out whether the problem's
negated conjecture was simplified out.

Definition at line 486 of file StackProver.hpp.

486 {
487 return negated_conjecture_removed;
488 }

◆ problem_has_true_conjecture()

bool StackProver::problem_has_true_conjecture ( ) const
inline

Find out whether the problem's conjecture
is $true.

Definition at line 464 of file StackProver.hpp.

464 {
465 return conjecture_true;
466 }

◆ problem_is_cnf_only()

bool StackProver::problem_is_cnf_only ( ) const
inline

Find out whether the problem is CNF only.

Definition at line 457 of file StackProver.hpp.

457 {
458 return cnf_only;
459 }

◆ process_axiom_forward()

void StackProver::process_axiom_forward ( )
private

Start a right branch to continue from an axiom.

You do this by taking the next available thing from the stack of right branches.

Definition at line 502 of file StackProver.cpp.

502 {
503 /*
504 * When you're moving forward in the search and you hit an axiom,
505 * you need to see whether there are right branches still needing
506 * to be dealt with.
507 *
508 * Note that an empty right_branch_stack - meaning that you've
509 * found a proof - is dealt with by go().
510 *
511 * this_action does not get populated for the new StackItem in
512 * this case.
513 */
514 right_branches_started++;
515 /*
516 * Move the next right branch to the stack.
517 */
518 stack.push_back(right_branch_stack.back());
519 right_branch_stack.pop_back();
520 /*
521 * Reset si.
522 */
523 si++;
524 /*
525 * Set up the new state.
526 */
527 new_C = stack[si].c;
528 path = stack[si].p;
529 lemmata = stack[si].l;
530 current_depth = stack[si].depth;
531 /*
532 * We deliberately delayed doing this, so do it now. (See
533 * documentation for StackProver::extend_with_action.)
534 */
535 populate_stack_item();
536 /*
537 * At this point you are starting a right branch, so
538 * if you are restricting backtracking you remove all
539 * alternatives from the relevant point in the stack.
540 */
541 if (params::limit_bt_extensions) {
542 stack[stack[si].bt_restriction_index].restrict_backtrack();
543 }
544}

◆ prove()

ProverOutcome StackProver::prove ( )

Here is where the magic happens.

You should only need to load the problem and call this method.

Make sure you deal with reordering.

Definition at line 1032 of file StackProver.cpp.

1032 {
1036 if (params::deterministic_reorder) {
1037 deterministic_reorder(params::number_of_reorders);
1038 }
1039 if (params::random_reorder) {
1040 random_reorder();
1041 }
1042 if (params::random_reorder_literals) {
1043 random_reorder_literals();
1044 }
1045 pair<bool, size_t> start_clause = matrix.find_start();
1046 /*
1047 * If the initial clauses don't have a positive and a negative
1048 * clause then the problem is trivial.
1049 */
1050 if (!start_clause.first) {
1051 return ProverOutcome::False;
1052 }
1053 /*
1054 * Deal with the possible ways to set up start clause(s) according to
1055 * the options. Keep track of which start clauses are in use, and if
1056 * necessary what outcomes for them have been seen so far.
1057 */
1058 set_up_start_clauses();
1059 /*
1060 * Main loop for iterative deepening search.
1061 */
1062 bool switched_to_complete = false;
1063 for (current_depth_limit = params::start_depth;
1064 current_depth_limit <= params::depth_limit;
1065 current_depth_limit += params::depth_increment) {
1066 /*
1067 * See if the parameters dictate that it's time to convert to
1068 * a complete search.
1069 */
1070 if (current_depth_limit >= params::switch_to_complete
1071 && !switched_to_complete) {
1072 params::set_complete_parameters();
1073 /*
1074 * You may have changed some parameters, so make sure all relevant
1075 * start clauses now get tried.
1076 */
1077 set_up_start_clauses();
1078 current_depth_limit = params::start_depth;
1079 switched_to_complete = true;
1080 colour_string::ColourString cs(params::use_colours);
1081 show.nl(1);
1082 show(1, cs("Switching to complete search.").orange(), true);
1083 }
1084 show.nl(1);
1085 show(1, string("SEARCH TO DEPTH: "));
1086 show(1, std::to_string(current_depth_limit), true);
1087 /*
1088 * Generate each possible start move, and try to prove from
1089 * it.
1090 */
1091 size_t start_clause_index = 0;
1092 for (const Clause& C : matrix) {
1093 /*
1094 * Find the next start clause.
1095 */
1096 if (results[start_clause_index] == StartClauseStatus::NoStart
1097 || results[start_clause_index] == StartClauseStatus::False) {
1098 start_clause_index++;
1099 continue;
1100 }
1101 /*
1102 * Reset everything to use the current start clause.
1103 *
1104 * TODO: this is slightly messy at present because
1105 * the var_index doesn't necessarily get reset in the
1106 * most efficient way possible if a previous schedule
1107 * attempt timed out. (You'd need to go back down
1108 * the stack and backtrack it as necessary.) This is
1109 * of course irrelevant
1110 * because it just means you might not get full re-use of
1111 * new variable names, but all the same it would be nice
1112 * to fix.
1113 */
1114 var_index.add_backtrack_point();
1115 new_C = C.make_copy_with_new_vars(var_index, term_index);
1116 reset_for_start();
1117 /*
1118 * Say what's going on.
1119 */
1120 show(1, string("START from clause "));
1121 show(1, std::to_string(start_clause_index + 1));
1122 show(1, string(" of "));
1123 show(1, std::to_string(matrix.get_num_clauses()));
1124 show(2, string(": "));
1125 show(2, new_C.to_string(), true);
1126 cout.flush();
1127 /*
1128 * Set up the initial stack item containing the start clause, and
1129 * populate it.
1130 */
1131 StackItem start_item(StackItemType::Start, new_C, path, lemmata, 1);
1132 start_item.set_this_action(InferenceItem(InferenceItemType::Start, start_clause_index));
1133 stack.push_back(start_item);
1134 si = 0;
1135 populate_stack_item();
1136 /*
1137 * Start with depth 1, as this makes sense when reading output if you're
1138 * using depth of recursion or path length.
1139 */
1140 current_depth = 1;
1141 /*
1142 * Liftoff!!!
1143 */
1144 ProverResult result = go();
1145 /*
1146 * Dealing with the outcome takes some care and depends on
1147 * the parameters being used.
1148 */
1149 switch (result) {
1150 case ProverResult::Valid:
1151 proof_count++;
1152 if (params::build_proof) {
1153 if (params::generate_LaTeX_proof) {
1154 proof_printer.make_LaTeX(params::LaTeX_proof_path,
1155 problem_path,
1156 matrix.make_LaTeX());
1157 }
1158 if (params::generate_Prolog_proof) {
1159 fs::path prolog_path = params::Prolog_proof_path;
1160 proof_printer.make_Prolog(prolog_path);
1161 matrix.write_to_prolog_file(params::Prolog_matrix_path);
1162 }
1163 }
1164 show(1, string(": Found proof number "));
1165 show(1, std::to_string(proof_count), true);
1166 return ProverOutcome::Valid;
1167 break;
1168 case ProverResult::Error:
1169 return ProverOutcome::Error;
1170 break;
1171 case ProverResult::TimeOut:
1172 return ProverOutcome::TimeOut;
1173 break;
1174 case ProverResult::OptionsExhausted:
1175 /*
1176 * If you ran out of options because you reached the depth
1177 * limit then you still need to continue.
1178 */
1179 if (depth_limit_reached) {
1180 show(1, string(": Depth limited"), true);
1181 }
1182 /*
1183 * If you ran out of options without reaching the depth limit, then
1184 * what you do depends on whether or not the search is complete.
1185 */
1186 else {
1187 if (params::search_is_complete()) {
1188 results[start_clause_index] = StartClauseStatus::False;
1189 show(1, string(": False"), true);
1190 }
1191 }
1192 start_clause_index++;
1193 break;
1194 default:
1195 return ProverOutcome::Error;
1196 break;
1197 }
1198 /*
1199 * This is necessary. Yes, I've checked. Think about it: you need
1200 * one extra backtrack to undo the new variables generated when you
1201 * make a start clause.
1202 */
1203 var_index.backtrack();
1204 }
1205 /*
1206 * Loop for start moves ends here.
1207 *
1208 * If everything was False then the theorem is False, otherwise
1209 * at least one attempt was depth-limited.
1210 */
1211 bool all_false = true;
1212 for (StartClauseStatus& outcome : results) {
1213 if (outcome == StartClauseStatus::Start) {
1214 all_false = false;
1215 break;
1216 }
1217 }
1218 if (all_false)
1219 return ProverOutcome::False;
1220 }
1221 /*
1222 * Iterative deepening loop ends here.
1223 */
1224 return ProverOutcome::PathLenLimit;
1225}
Clause::to_string
string to_string(bool=false) const
Convert to a string.
Definition Clause.cpp:244
Matrix::get_num_clauses
ClauseNum get_num_clauses() const
Straightforward get method.
Definition Matrix.hpp:225
Matrix::make_LaTeX
string make_LaTeX(bool=false) const
Make a usable LaTeX representation.
Definition Matrix.cpp:259
Matrix::write_to_prolog_file
void write_to_prolog_file(const path &) const
Write to a file that can be read by Prolog.
Definition Matrix.cpp:272
Matrix::find_start
pair< bool, size_t > find_start() const
Use a simple heuristic to find a good start clause.
Definition Matrix.cpp:54
ProofPrinter::make_Prolog
void make_Prolog(const path &)
Convert to a form suitable for use by the Prolog proof checker and write to a file.
Definition ProofPrinter.cpp:168
ProofPrinter::make_LaTeX
void make_LaTeX(const path &, const path &, const string &)
Convert to LaTeX and store in the specified file.
Definition ProofPrinter.cpp:116
StackProver::reset_for_start
void reset_for_start()
Reset everything so that you can start from a specified start clause.
Definition StackProver.hpp:307
StackProver::random_reorder
void random_reorder()
Randomly reorder the matrix.
Definition StackProver.hpp:430
StackProver::set_up_start_clauses
void set_up_start_clauses()
The start clauses to use depend on the settings, and the settings can change.
Definition StackProver.cpp:905
StackProver::go
ProverResult go()
This runs the proof search from a given Start Move.
Definition StackProver.cpp:652
StackProver::deterministic_reorder
void deterministic_reorder(uint32_t n)
Deterministically reorder the matrix n times.
Definition StackProver.hpp:424
StackProver::random_reorder_literals
void random_reorder_literals()
Randomly reorder the literals in each clause in the matrix.
Definition StackProver.hpp:437
colour_string::ColourString
Simple addition of colour to strings and ostreams.
Definition vic_strings.hpp:121
verbose_print::VPrint::nl
void nl(uint8_t, uint8_t=1)
Definition vic_strings.cpp:142
InferenceItem
Full representation of inferences, beyond just the name.
Definition InferenceItem.hpp:61
StackItem
Stack items: each contains its own material for generating possible next inferences.
Definition StackItem.hpp:56
params::set_complete_parameters
static void set_complete_parameters()
Change the parameters to make the search complete.
Definition Parameters.cpp:215
params::search_is_complete
static bool search_is_complete()
Self-explanatory.
Definition Parameters.cpp:227

◆ random_reorder()

void StackProver::random_reorder ( )
inline

Randomly reorder the matrix.

Definition at line 430 of file StackProver.hpp.

430 {
431 matrix.random_reorder();
432 }
Matrix::random_reorder
void random_reorder()
Randomly reorder the matrix.
Definition Matrix.cpp:164

◆ random_reorder_literals()

void StackProver::random_reorder_literals ( )
inline

Randomly reorder the literals in each clause in the matrix.

Definition at line 437 of file StackProver.hpp.

437 {
438 matrix.random_reorder_literals();
439 }
Matrix::random_reorder_literals
void random_reorder_literals()
Randomly reorder the literals in each clause in the matrix.
Definition Matrix.cpp:190

◆ read_from_tptp_file()

void StackProver::read_from_tptp_file ( const string & file_name,
bool & found_conjecture,
size_t & fof_size )

Obviously, reads a problem from a TPTP file.

Does pretty much all of the setup required.

Parameters
file_nameName of the file to use.
found_conjectureUsed to indicate whether a conjecture is found in the problem.
fof_sizeNumber of first-order formulas found.

Definition at line 78 of file StackProver.cpp.

80 {
81 TPTPParser parser(&var_index, &fun_index, &term_index, &pred_index, &matrix);
82 parser.parse_tptp_from_file(file_name);
83 status = parser.get_problem_status();
84 bool equality = parser.equality_used();
85 found_conjecture = parser.conjecture_present();
86 fof_size = parser.number_of_fof_formulas();
87 Predicate* equals_predicate = parser.get_equals_predicate();
88 cnf_only = parser.problem_is_cnf_only();
89 conjecture_true = parser.fof_conjecture_is_true();
90 conjecture_false = parser.fof_conjecture_is_false();
91 conjecture_missing = parser.fof_conjecture_is_missing();
92 negated_conjecture_removed = parser.fof_negated_conjecture_removed();
93 fof_has_axioms = parser.fof_has_axioms();
94 simplified_fof_has_axioms = parser.simplified_fof_has_axioms();
95 tptp_conversion_string = parser.get_tptp_conversion_string();
96 parser.clear();
97 num_preds = pred_index.get_num_preds();
98 /*
99 * num_preds for Matrix is set by parser.
100 */
101 path.set_num_preds(num_preds);
102
103 if (params::show_clauses) {
104 std::exit(EXIT_SUCCESS);
105 }
106
107 if (status != string("") && params::first_parse) {
108 show(1, string("Problem status found: "));
109 show(1, status, true);
110 }
111 if (equality && params::add_equality_axioms) {
112 if (params::first_parse) {
113 show(1, string("Problem involves equality: adding axioms for =."), true);
114 params::first_parse = false;
115 }
116 add_equality_axioms(equals_predicate);
117 if (params::equality_axioms_at_start) {
118 matrix.move_equals_to_start();
119 }
120 }
121 /*
122 * Any further variables will be anonymous.
123 */
124 var_index.set_all_names_added();
125 }
Matrix::move_equals_to_start
void move_equals_to_start()
Self-explanatory.
Definition Matrix.cpp:208
StackProver::add_equality_axioms
void add_equality_axioms(Predicate *)
After reading a problem in which = and/or != appears, add the axioms for equality.
Definition StackProver.cpp:127
TPTPParser
Wrap up everything the TPTP parser needs to do inside a single class.
Definition TPTPParser.hpp:658
VariableIndex::set_all_names_added
void set_all_names_added()
Call this to indicate that only anonymous variables can now be created.
Definition VariableIndex.cpp:63

◆ reduction_backtrack()

void StackProver::reduction_backtrack ( )
private

One of several different kinds of backtracking.

Definition at line 553 of file StackProver.cpp.

553 {
554 sub_stack.backtrack();
555 backtrack_once();
556}

◆ reset_for_start()

void StackProver::reset_for_start ( )
inlineprivate

Reset everything so that you can start from a specified start clause.

Definition at line 307 of file StackProver.hpp.

307 {
308 depth_limit_reached = false;
309 si = 0;
310 backtrack = false;
311 path.clear();
312 stack.clear();
313 lemmata.clear();
314 right_branch_stack.clear();
315 sub_stack.clear();
316 }
Lemmata::clear
void clear()
Self-explanatory.
Definition Lemmata.hpp:70
SubstitutionStack::clear
void clear()
Reset everything.
Definition SubstitutionStack.hpp:91

◆ right_extension_backtrack()

void StackProver::right_extension_backtrack ( )
private

One of several different kinds of backtracking.

Here be DRAGONS.

Care needed here. If the state is a right branch, then it may or may not have to go back on right_branch_stack as you may or may not need to try it again, depending on the settings.

If you get this wrong you get a REALLY evil bug, because with the standard restricted backtracking you put it back on the stack when it's not needed. You then end up with extra things in the proof certificate which invalidate it, even though you can take them out and possibly get something valid.

Guess how I know this!

Definition at line 590 of file StackProver.cpp.

590 {
591 /*
592 * If you're not limiting backtracking for extensions, or
593 * you *are*, but you're still exploring left trees, then this
594 * is straightforward: just put the item back on right_branch_stack
595 * so that it gets explored again later.
596 */
597 if (!params::limit_bt_extensions ||
598 ((params::limit_bt_extensions || params::limit_bt_all) &&
599 !params::limit_bt_extensions_left_tree)) {
600 /*
601 * Why is this necessary? After we backtrack we may make different
602 * substitutions, so in revisiting the right branch different
603 * possibilties may apply, so we re-compute them later.
604 */
605 stack.back().clear();
606 right_branch_stack.push_back(stack.back());
607 backtrack_once();
608 return;
609 }
610 /*
611 * We know we are limiting backtracking for extensions, and we
612 * are not exploring the left tree.
613 *
614 * Care is needed if you're not backtracking within the left
615 * part of the tree. You need to move back down the stack,
616 * deleting everything while also making sure that sub_stack
617 * and var_index are correctly maintained. Also, you don't
618 * want to return anything to right_branch_stack.
619 *
620 * This goes back to where the relevant literal was selected.
621 * Thus if you are not limiting the possibilities to only those
622 * for the first literal, it's open to the backtracking
623 * restriction to leave other possibilites to be tried, and
624 * they get picked up from this point.
625 */
626 if (params::limit_bt_extensions_left_tree) {
627 size_t target_index = stack[si].bt_restriction_index;
628 size_t current_index = stack.size() - 1;
629 while (current_index > target_index) {
630 switch (stack[si].item_type) {
631 case StackItemType::Lemmata:
632 break;
633 case StackItemType::Reduction:
634 sub_stack.backtrack();
635 break;
636 case StackItemType::LeftBranch:
637 var_index.backtrack();
638 sub_stack.backtrack();
639 break;
640 case StackItemType::RightBranch:
641 break;
642 default:
643 cerr << "Something is VERY WRONG!" << endl;
644 break;
645 }
646 backtrack_once();
647 current_index--;
648 }
649 }
650}

◆ set_num_preds()

void StackProver::set_num_preds ( size_t n)

Set the number of predicates.

But don't! You should never need to do this.

Definition at line 72 of file StackProver.cpp.

72 {
73 num_preds = n;
74 matrix.set_num_preds(n);
75 path.set_num_preds(n);
76}
Matrix::set_num_preds
void set_num_preds(size_t)
Make an empty index.
Definition Matrix.cpp:44

◆ set_problem_path()

void StackProver::set_problem_path ( fs::path & p)
inline

Set the path for the problem being solved.

Used only to produce nice output.

Definition at line 391 of file StackProver.hpp.

391{ problem_path = p; }

◆ set_timeout()

void StackProver::set_timeout ( chrono::steady_clock::time_point time)
inline

Set a timeout.

A StackProver is always constructed to have no timeout. This sets a timeout to use in seconds. The parameters are separate from the params::???? values as the latter apply globally whereas these allow for schedules to be constructed.

Parameters
timethe time to stop: you will need to know about the standard library!

Definition at line 382 of file StackProver.hpp.

382 {
383 use_timeout = true;
384 end_time = time;
385 }

◆ set_up_start_clauses()

void StackProver::set_up_start_clauses ( )
private

The start clauses to use depend on the settings, and the settings can change.

Definition at line 905 of file StackProver.cpp.

905 {
906 results.clear();
907 size_t m_size = matrix.get_num_clauses();
908 /*
909 * Make sure noone has messed up and not set any start
910 * clause optionss.
911 */
912 if (params::no_start_options())
913 params::correct_missing_start_options();
914 /*
915 * The allstart option overides everything else so this is easy.
916 */
917 if (params::all_start) {
918 for (size_t i = 0; i < m_size; i++) {
919 results.push_back(StartClauseStatus::Start);
920 }
921 return;
922 }
923 bool first_clause_included = false;
924 /*
925 * params::all_pos_neg_start indicates use of positive
926 * or negative start clauses according to the representation.
927 * When you don't also have conjecture_start, either include
928 * all, or just the first possibility found.
929 */
930 if (params::all_pos_neg_start && !params::conjecture_start) {
931 for (size_t i = 0; i < m_size; i++) {
932 if (
933 (
934 (params::positive_representation && matrix.is_positive(i))
935 ||
936 (!params::positive_representation && matrix.is_negative(i))
937 )
938 &&
939 (!(params::restrict_start && first_clause_included))
940 ) {
941 results.push_back(StartClauseStatus::Start);
942 first_clause_included = true;
943 }
944 else {
945 results.push_back(StartClauseStatus::NoStart);
946 }
947 }
948 }
949 /*
950 * Similar case if you have conjecture_start but not all_pos_neg_start.
951 */
952 else if (!params::all_pos_neg_start && params::conjecture_start) {
953 for (size_t i = 0; i < m_size; i++) {
954 if (matrix.is_conjecture(i)
955 &&
956 (!(params::restrict_start && first_clause_included))) {
957 results.push_back(StartClauseStatus::Start);
958 first_clause_included = true;
959 }
960 else {
961 results.push_back(StartClauseStatus::NoStart);
962 }
963 }
964 }
965 /*
966 * The tricky case is when you want to combine pos/neg clauses,
967 * conjecture clauses, and restriction in some other way.
968 *
969 * Assume here that you have all_pos_neg_start and conjecture_start.
970 */
971 else {
972 for (size_t i = 0; i < m_size; i++) {
973 if (matrix.is_conjecture(i)
974 &&
975 (
976 (params::positive_representation && matrix.is_positive(i))
977 ||
978 (!params::positive_representation && matrix.is_negative(i))
979 )
980 &&
981 !(params::restrict_start && first_clause_included)) {
982 results.push_back(StartClauseStatus::Start);
983 first_clause_included = true;
984 }
985 else {
986 results.push_back(StartClauseStatus::NoStart);
987 }
988 }
989 }
990 /*
991 * There's a rare possibility that---because either there was no
992 * (negated) conjecture clause in the problem, or they were
993 * simplified out---at this point no start clause has been
994 * selected. If that's the case, either use all positive/negative
995 * clauses or just the first, according to the parameters set.
996 *
997 * Note: this must choose at least one start clause because problems
998 * without a positive and negative clause have already been solved.
999 */
1000 if (!first_clause_included) {
1001 if (params::verbosity > 2) {
1002 cout << "Note: you're asking for a conjecture to start, but there are none!" << endl;
1003 cout << " depending on the other parameter settings, we will use one or " << endl;
1004 cout << " all of the negative clauses." << endl;
1005 }
1006 // Don't forget this! If you get here you have a whole bunch of
1007 // NoStart in results!
1008 results.clear();
1009 for (size_t i = 0; i < m_size; i++) {
1010 if ((
1011 (params::positive_representation && matrix.is_positive(i))
1012 ||
1013 (!params::positive_representation && matrix.is_negative(i))
1014 ) &&
1015 !(params::restrict_start && first_clause_included)) {
1016 results.push_back(StartClauseStatus::Start);
1017 first_clause_included = true;
1018 }
1019 else {
1020 results.push_back(StartClauseStatus::NoStart);
1021 }
1022 }
1023 }
1024}
Matrix::is_negative
bool is_negative(size_t i) const
Is a particular Clause negative?
Definition Matrix.hpp:279
Matrix::is_conjecture
bool is_conjecture(size_t i) const
Is a particular Clause a conjecture?
Definition Matrix.cpp:49
Matrix::is_positive
bool is_positive(size_t i) const
Is a particular Clause positive?
Definition Matrix.hpp:273
params::no_start_options
static bool no_start_options()
Self-explanatory.
Definition Parameters.cpp:247
params::correct_missing_start_options
static void correct_missing_start_options()
Self-explanatory.
Definition Parameters.cpp:254

◆ show_full_statistics()

void StackProver::show_full_statistics ( size_t ms) const

Display counts of number of extensions tried and so on, as well as numbers per second.

Definition at line 1263 of file StackProver.cpp.

1263 {
1264 size_t total = reductions_tried + extensions_tried + lemmata_tried + right_branches_started;
1265 double s = static_cast<double>(ms) / 1000.0;
1266 double ext_rate = (static_cast<double>(extensions_tried) / s);
1267 double red_rate = (static_cast<double>(reductions_tried) / s);
1268 double lem_rate = (static_cast<double>(lemmata_tried) / s);
1269 double right_rate = (static_cast<double>(right_branches_started) / s);
1270 double total_rate = (static_cast<double>(total) / s);
1271 cout << "Reductions: " << setw(15) << reductions_tried << " (" << static_cast<size_t>(red_rate) << "/s)" << endl;
1272 cout << "Extensions: " << setw(15) << extensions_tried << " (" << static_cast<size_t>(ext_rate) << "/s)" << endl;
1273 cout << "Lemmas: " << setw(15) << lemmata_tried << " (" << static_cast<size_t>(lem_rate) << "/s)" << endl;
1274 cout << "Right branches: " << setw(15) << right_branches_started << " (" << static_cast<size_t>(right_rate) << "/s)" << endl;
1275 cout << "Total: " << setw(15) << total << " (" << static_cast<size_t>(total_rate) << "/s)" << endl;
1276}

◆ show_matrix() [1/2]

void StackProver::show_matrix ( )
inline

Show a nicely formatted matrix.

Definition at line 443 of file StackProver.hpp.

443 {
444 cout << "Matrix:" << endl;
445 cout << matrix.to_string() << endl;
446 }
Matrix::to_string
string to_string() const
Make a string representation.
Definition Matrix.cpp:236

◆ show_matrix() [2/2]

void StackProver::show_matrix ( ) const
inline

Definition at line 540 of file StackProver.hpp.

540{ cout << matrix << endl; }

◆ show_path()

void StackProver::show_path ( ) const
inline

Definition at line 541 of file StackProver.hpp.

541{ cout << path << endl; }

◆ show_right_stack()

void StackProver::show_right_stack ( )

Definition at line 1241 of file StackProver.cpp.

1241 {
1242 cout << "--------------------------------------------------------" << endl;
1243 cout << "Right Stack:" << endl;
1244 cout << "--------------------------------------------------------" << endl;
1245 for (auto s : right_branch_stack) {
1246 cout << s << endl;
1247 }
1248 cout << "--------------------------------------------------------" << endl;
1249}

◆ show_stack()

void StackProver::show_stack ( )

Definition at line 1231 of file StackProver.cpp.

1231 {
1232 cout << "--------------------------------------------------------" << endl;
1233 cout << "Stack:" << endl;
1234 cout << "--------------------------------------------------------" << endl;
1235 for (auto s : stack) {
1236 cout << s << endl;
1237 }
1238 cout << "--------------------------------------------------------" << endl;
1239}

◆ show_statistics()

void StackProver::show_statistics ( ) const

Display counts of number of extensions tried and so on.

Definition at line 1251 of file StackProver.cpp.

1251 {
1252 verbose_print::VPrint show(params::verbosity);
1253 show(1, string("Reductions: "));
1254 show(1, std::to_string(reductions_tried));
1255 show(1, string(" Extensions: "));
1256 show(1, std::to_string(extensions_tried));
1257 show(1, string(" Lemmata: "));
1258 show(1, std::to_string(lemmata_tried));
1259 show(1, string(" Right branches: "));
1260 show(1, std::to_string(right_branches_started), true);
1261}
verbose_print::VPrint
Definition vic_strings.hpp:240

◆ show_term_index()

void StackProver::show_term_index ( )
inline

Definition at line 544 of file StackProver.hpp.

544{ cout << term_index << endl; }

◆ show_tptp_proof()

void StackProver::show_tptp_proof ( )
inline

Show a Prolog-formatted proof.

Definition at line 509 of file StackProver.hpp.

509 {
510 cout << endl << "% Problem matrix:" << endl;
511 matrix.show_tptp();
512 cout << endl << "% Proof stack:" << endl;
513 proof_printer.show_tptp();
514 }
Matrix::show_tptp
void show_tptp() const
Output in TPTP compatible format.
Definition Matrix.cpp:289
ProofPrinter::show_tptp
void show_tptp()
Show the proof in a TPTP-friendly format.
Definition ProofPrinter.cpp:282

◆ simplified_problem_has_fof_axioms()

bool StackProver::simplified_problem_has_fof_axioms ( ) const
inline

Find out from the parser whether the problem had axioms after simplification.

Definition at line 500 of file StackProver.hpp.

500 {
501 return simplified_fof_has_axioms;
502 }

Friends And Related Symbol Documentation

◆ operator<<

ostream & operator<< ( ostream & out,
const StackProver & p )
friend

Definition at line 1278 of file StackProver.cpp.

1278 {
1279 out << "Current state of the RecursiveProver object" << endl;
1280 out << "-------------------------------------------" << endl << endl;
1281 out << p.var_index << endl;
1282 out << p.fun_index << endl;
1283 out << p.term_index << endl;
1284 out << p.path << endl;
1285 out << p.matrix << endl;
1286 return out;
1287}

Member Data Documentation

◆ action

InferenceItem StackProver::action
private

Stores the next action from the current StackItem.

Definition at line 146 of file StackProver.hpp.

◆ backtrack

bool StackProver::backtrack
private

Are we moving up or down the stack?

Definition at line 185 of file StackProver.hpp.

◆ cnf_only

bool StackProver::cnf_only
private

Keep track of whether there were any FOF formulas in the problem file.

Definition at line 321 of file StackProver.hpp.

◆ conjecture_false

bool StackProver::conjecture_false
private

Keep track of whether the parser found the conjecture to be false.

Definition at line 329 of file StackProver.hpp.

◆ conjecture_missing

bool StackProver::conjecture_missing
private

Keep track of whether the parser found a conjecture in the problem file.

Definition at line 333 of file StackProver.hpp.

◆ conjecture_true

bool StackProver::conjecture_true
private

Keep track of whether the parser found the conjecture to be true.

Definition at line 325 of file StackProver.hpp.

◆ current_depth

uint32_t StackProver::current_depth
private

Self-explanatary.

Definition at line 158 of file StackProver.hpp.

◆ current_depth_limit

uint32_t StackProver::current_depth_limit
private

Self-explanatary.

Definition at line 154 of file StackProver.hpp.

◆ depth_limit_reached

bool StackProver::depth_limit_reached
private

Self-explanatary.

Definition at line 162 of file StackProver.hpp.

◆ end_time

chrono::steady_clock::time_point StackProver::end_time
private

When do we stop because of a timeout?

Definition at line 234 of file StackProver.hpp.

◆ extensions_tried

uint32_t StackProver::extensions_tried = 0
staticprivate

We'll be keeping some simple statistics about the search process.

Definition at line 211 of file StackProver.hpp.

◆ fof_has_axioms

bool StackProver::fof_has_axioms
private

Keep track of whether the parser found that it's an FOF problem with axioms before simplification.

Definition at line 342 of file StackProver.hpp.

◆ fun_index

FunctionIndex StackProver::fun_index
private

This class needs one of each kind of index to keep track of Variables, Terms etc.

Definition at line 90 of file StackProver.hpp.

◆ lemmata

Lemmata StackProver::lemmata
private

At any point in the search process this is a copy of the list of lemmas for the current node in the proof being constructed.

Definition at line 138 of file StackProver.hpp.

◆ lemmata_tried

uint32_t StackProver::lemmata_tried = 0
staticprivate

We'll be keeping some simple statistics about the search process.

Definition at line 216 of file StackProver.hpp.

◆ matrix

Matrix StackProver::matrix
private

A copy of the matrix you're working with.

Definition at line 120 of file StackProver.hpp.

◆ negated_conjecture_removed

bool StackProver::negated_conjecture_removed
private

Keep track of whether the parser simplified the conjecture away.

Definition at line 337 of file StackProver.hpp.

◆ new_C

Clause StackProver::new_C
private

At any point in the search process this is a copy of the clause for the current node in the proof being constructed.

Definition at line 132 of file StackProver.hpp.

◆ num_preds

size_t StackProver::num_preds
private

How many prdicates does the problem of interest have?

Definition at line 80 of file StackProver.hpp.

◆ output_interval

Interval StackProver::output_interval
private

How often do you output updates about progress?

Definition at line 198 of file StackProver.hpp.

◆ path

SimplePath StackProver::path
private

At any point in the search process this is a copy of the path for the current node in the proof being constructed.

Definition at line 126 of file StackProver.hpp.

◆ pred_index

PredicateIndex StackProver::pred_index
private

This class needs one of each kind of index to keep track of Variables, Terms etc.

Definition at line 100 of file StackProver.hpp.

◆ problem_path

fs::path StackProver::problem_path
private

Path for the problem of interest.

Definition at line 194 of file StackProver.hpp.

◆ proof_count

uint32_t StackProver::proof_count
private

If we're searching for multiple proofs, keep count
of which one this is.

Definition at line 226 of file StackProver.hpp.

◆ proof_printer

ProofPrinter StackProver::proof_printer
private

You need one of these to print LaTeX output or any kind of proof certificate.

Definition at line 190 of file StackProver.hpp.

◆ reductions_tried

uint32_t StackProver::reductions_tried = 0
staticprivate

We'll be keeping some simple statistics about the search process.

Note that at present these statistics include everything tried over all steps in a schedule.

Definition at line 206 of file StackProver.hpp.

◆ results

vector<StartClauseStatus> StackProver::results
private

This is populated by the StackProver::set_up_start_clauses method.

That method looks at the settings for start clauses and tries to achieve them all in a sensible way. Initially this indicates which clauses to use to start, but then stores the results obtained after trying each possibility.

Definition at line 116 of file StackProver.hpp.

◆ right_branch_stack

vector<StackItem> StackProver::right_branch_stack
private

We build the proof by trying the left branches of extensions first: this stack keeps track of the right branches that we need to come back to.

Definition at line 181 of file StackProver.hpp.

◆ right_branches_started

uint32_t StackProver::right_branches_started = 0
staticprivate

We'll be keeping some simple statistics about the search process.

Definition at line 221 of file StackProver.hpp.

◆ show

verbose_print::VPrint StackProver::show
private

Set up printing according to verbosity.

Definition at line 238 of file StackProver.hpp.

◆ si

size_t StackProver::si
private

Index of the current StackItem.

Definition at line 150 of file StackProver.hpp.

◆ simplified_fof_has_axioms

bool StackProver::simplified_fof_has_axioms
private

Keep track of whether the parser found that it's an FOF problem with axioms after simplification.

Definition at line 347 of file StackProver.hpp.

◆ stack

vector<StackItem> StackProver::stack
private

Main stack: this is constructed by the search process and, if completed, represents a proof.

Definition at line 175 of file StackProver.hpp.

◆ status

string StackProver::status
private

Problem status, if found in input file.

Definition at line 166 of file StackProver.hpp.

◆ sub_stack

SubstitutionStack StackProver::sub_stack
private

There is a separate stack to make application and removal of substitutions straightforward.

Definition at line 105 of file StackProver.hpp.

◆ term_index

TermIndex StackProver::term_index
private

This class needs one of each kind of index to keep track of Variables, Terms etc.

Definition at line 95 of file StackProver.hpp.

◆ tptp_conversion_string

string StackProver::tptp_conversion_string
private

TPTP-friendly description of the clause conversion.

Definition at line 170 of file StackProver.hpp.

◆ u

Unifier StackProver::u
private

We need a single Unifier to use throughout the process.

Definition at line 142 of file StackProver.hpp.

◆ use_timeout

bool StackProver::use_timeout
private

Are we using a timeout?

Definition at line 230 of file StackProver.hpp.

◆ var_index

VariableIndex StackProver::var_index
private

This class needs one of each kind of index to keep track of Variables, Terms etc.

Definition at line 85 of file StackProver.hpp.

The documentation for this class was generated from the following files: