Matrix Class Reference

Representation of the Matrix within a proof. More...

#include <Matrix.hpp>

Collaboration diagram for Matrix:

Public Member Functions
	Matrix ()
	Use this constructor if you really want an empty Matrix.
	Matrix (size_t)
	Use this constructor when you know how many predicates there are.
	Matrix (const Matrix &)=delete
	You're never going to need to copy a Matrix.
	Matrix (const Matrix &&)=delete
Matrix &	operator= (const Matrix &)=delete
Matrix &	operator= (const Matrix &&)=delete
ClauseNum	get_num_clauses () const
	Straightforward get method.
const Clause &	operator[] (size_t i) const
	Straightforward get method.
bool	is_positive (size_t i) const
	Is a particular Clause positive?.
bool	is_negative (size_t i) const
	Is a particular Clause negative?.
bool	is_conjecture (size_t i) const
	Is a particular Clause a conjecture?
void	set_num_equals (uint32_t n)
	Straightforward set method.
pair< bool, size_t >	find_start () const
	Use a simple heuristic to find a good start clause.
void	set_num_preds (size_t)
	Make an empty index.
void	add_clause (Clause &, string="")
	Add a Clause to the Matrix and update the index accordingly.
void	find_limited_extensions (Unifier &, vector< InferenceItem > &, Clause &, VariableIndex &, TermIndex &)
	Find all possible extensions given a Clause, but only consider the first Literal in the Clause.
void	find_all_extensions (Unifier &, vector< InferenceItem > &, Clause &, VariableIndex &, TermIndex &)
	Find all possible extensions given a Clause, considering all Literals in the Clause.
void	deterministic_reorder (size_t)
	Deterministic reorder of the clauses.
void	random_reorder ()
	Randomly reorder the matrix.
void	random_reorder_literals ()
	Randomly reorder the literals in each clause in the matrix.
void	move_equals_to_start ()
	Self-explanatory.
vector< Clause >::const_iterator	cbegin () const
vector< Clause >::const_iterator	cend () const
vector< Clause >::iterator	begin ()
vector< Clause >::iterator	end ()
string	to_string () const
	Make a string representation.
string	make_LaTeX (bool=false) const
	Make a usable LaTeX representation.
void	write_to_prolog_file (const path &) const
	Write to a file that can be read by Prolog.
void	show_tptp () const
	Output in TPTP compatible format.
void	sort_clauses_by_increasing_size ()
	Self-explanatory.

Private Member Functions
void	find_extensions (Unifier &, vector< InferenceItem > &, const Literal &, LitNum, VariableIndex &, TermIndex &)
	Find all possible extensions, given a Literal.
void	make_clauses_copy ()
	Store a copy of the clauses.
template<class Comparison >
void	sort_clauses (Comparison comparison)
	Template method for general sorting of clauses, which sorts roles at the same time.

Private Attributes
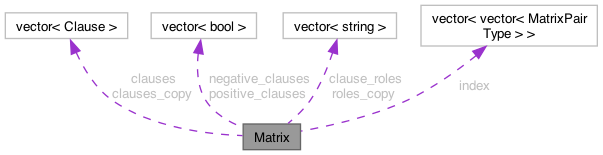
vector< Clause >	clauses
	The Matrix itself is just a set of Clauses.
vector< bool >	positive_clauses
	Keep track of which clauses are positive.
vector< bool >	negative_clauses
	Keep track of which clauses are negative.
vector< string >	clause_roles
	Keep track of which clauses are conjectures etc.
uint32_t	num_equals
	You need to know how many equality axioms there are in case you want to move them around.
vector< Clause >	clauses_copy
	It makes sense to keep a copy of the clauses if your schedule reorders multiple times.
vector< string >	roles_copy
	It makes sense to keep a copy of the roles if your schedule reorders multiple times.
bool	copy_saved
	Remember whether you've saved a copy.
vector< vector< MatrixPairType > >	index
	We want to be able to quickly identify where in each clause a particular literal lives.

Static Private Attributes
static std::mt19937	d
	Randomness for random reordering.

Friends
ostream &	operator<< (ostream &, const Matrix &)

Detailed Description

Representation of the Matrix within a proof.

The Matrix itself never actually changes. However we do want to be able to look things up quickly when finding possible extension steps, so we build an index to help with that.

This class is also the natural place to implement the finding of all extensions, and the start clause heuristics.

Definition at line 73 of file Matrix.hpp.

Constructor & Destructor Documentation

Matrix() [1/3]

Matrix::Matrix ( )

inline

Use this constructor if you really want an empty Matrix.

Definition at line 198 of file Matrix.hpp.

    : clauses()
    , index()
    , positive_clauses()
    , negative_clauses()
    , clause_roles()
    , clauses_copy()
    , roles_copy()
    , copy_saved(false)
    {}

Matrix() [2/3]

Matrix::Matrix

(

size_t

num_predicates

)

Use this constructor when you know how many predicates there are.

Parameters

num_predicates

Number of predicates.

Definition at line 30 of file Matrix.cpp.

: clauses()
, index((num_predicates * 2), vector<MatrixPairType>())
, positive_clauses()
, negative_clauses()
, clause_roles()
, num_equals(0)
, clauses_copy()
, roles_copy()
, copy_saved(false)
{}

Matrix() [3/3]

Matrix::Matrix ( const Matrix & )

delete

You're never going to need to copy a Matrix.

Let the compiler be your friend.

Member Function Documentation

add_clause()

void Matrix::add_clause	(	Clause &	clause,
		string	role = "" )

Add a Clause to the Matrix and update the index accordingly.

Optionally add a clause role.

Parameters

clause	Reference to the Clause.
role	A string denoting the role of the clause.

Definition at line 91 of file Matrix.cpp.

                                                   {
    ClauseNum clause_number = clauses.size();
    LitNum literal_number = 0;
    for (size_t j = 0; j < clause.size(); j++) {
        size_t i = clause[j].get_pred_as_index();
        index[i].push_back(MatrixPairType(clause_number, literal_number));
        literal_number++;
    }
    clauses.push_back(clause);
    positive_clauses.push_back(clause.is_positive());
    negative_clauses.push_back(clause.is_negative());
    clause_roles.push_back(role);
}

begin()

vector< Clause >::iterator Matrix::begin ( )

inline

Definition at line 345 of file Matrix.hpp.

{ return clauses.begin(); }

cbegin()

vector< Clause >::const_iterator Matrix::cbegin ( ) const

inline

Definition at line 343 of file Matrix.hpp.

{ return clauses.cbegin(); }

cend()

vector< Clause >::const_iterator Matrix::cend ( ) const

inline

Definition at line 344 of file Matrix.hpp.

{ return clauses.cend(); }

deterministic_reorder()

void Matrix::deterministic_reorder

(

size_t

n

)

Deterministic reorder of the clauses.

Call the reorder algorithm the specified number of times. This assumes you have stored a copy of the original clauses.

Parameters

n	Number of times to call the reorder algorithm

Only store a copy of the clauses the first time you do this.

Definition at line 105 of file Matrix.cpp.

                                           {
  if (!copy_saved) {
    copy_saved = true;
    make_clauses_copy();
  }
  /*
  * Find a suitably reordered set of indices.
  */
  vector<uint32_t> new_order;
  size_t s = clauses.size();
  for (size_t i = 0; i < s; i++)
    new_order.push_back(i);
  new_order = deterministic_reorder_n_times<uint32_t>(new_order, n);
  /*
  * Clear and rebuild as necessary.
  */
  clauses.clear();
  positive_clauses.clear();
  negative_clauses.clear();
  clause_roles.clear();
  size_t s2 = index.size();
  index.clear();
  index = vector<vector<MatrixPairType> >(s2, vector<MatrixPairType>());
  for (size_t i = 0; i < s; i++) {
    add_clause(clauses_copy[new_order[i]], roles_copy[new_order[i]]);
  }
}

end()

vector< Clause >::iterator Matrix::end ( )

inline

Definition at line 346 of file Matrix.hpp.

{ return clauses.end(); }

find_all_extensions()

void Matrix::find_all_extensions	(	Unifier &	u,
		vector< InferenceItem > &	result,
		Clause &	c,
		VariableIndex &	var_index,
		TermIndex &	term_index )

Find all possible extensions given a Clause, considering all Literals in the Clause.

See the documentation for find_extensions, which does all the heavy lifting.

Parameters

u	A reference to a Unifier function object.
result	A reference to a vector of InferenceItems. Start with this empty.
c	The Clause of interest.
var_index	A reference to the VariableIndex.
term_index	A reference to the TermIndex.

Definition at line 238 of file Matrix.cpp.

                                                {
  if (c.size() == 0) {
    cerr << "You shouldn't be looking for extensions with an empty clause" << endl;
    return;
  }
  for (size_t index = 0; index < c.size(); index++) {
      find_extensions(u, result, c[index], index, var_index, term_index);
  }
}

find_extensions()

void Matrix::find_extensions ( Unifier & u, vector< InferenceItem > & result, const Literal & lit, LitNum ind, VariableIndex & var_index, TermIndex & term_index )

private

Find all possible extensions, given a Literal.

Essentially this involves finding all the Clauses in the Matrix containing a Literal complementary to the one of interest, and selecting each of those Literals that unifies with the one of interest. You can do this by traversing a single row of the index.

It's up to the caller to decide whether to clear the result.

Parameters

u	Reference to a Unifier function object.
result	Reference to a vector of InferenceItems.
lit	Reference to the Literal of interest.
ind	the index (position) of the Literal in its Clause.
var_index	Reference to the VariableIndex.
term_index	Reference to the TermIndex.

Definition at line 207 of file Matrix.cpp.

                                                                              {
    Literal neg_lit(lit);
    neg_lit.invert();
    size_t i = neg_lit.get_pred_as_index();
    for (const MatrixPairType& p : index[i]) {
        ClauseNum c_num = p.first;
        LitNum l_num = p.second;
        var_index.add_backtrack_point();
        Clause new_c = (clauses[c_num]).make_copy_with_new_vars(var_index, term_index);
        UnificationOutcome outcome = u(neg_lit, new_c[l_num]);
        if (outcome == UnificationOutcome::Succeed) {
            result.push_back(InferenceItem(InferenceItemType::Extension, lit, ind,
                            c_num, l_num, u.get_substitution()));
        }
        var_index.backtrack();
        u.backtrack();
    }
}

find_limited_extensions()

void Matrix::find_limited_extensions	(	Unifier &	u,
		vector< InferenceItem > &	result,
		Clause &	c,
		VariableIndex &	var_index,
		TermIndex &	term_index )

Find all possible extensions given a Clause, but only consider the first Literal in the Clause.

See the documentation for find_extensions, which does all the heavy lifting.

Parameters

u	A reference to a Unifier function object.
result	A reference to a vector of InferenceItems. Start with this empty.
c	The Clause of interest.
var_index	A reference to the VariableIndex.
term_index	A reference to the TermIndex.

Definition at line 228 of file Matrix.cpp.

                                                {
  if (c.size() == 0) {
    cerr << "You shouldn't be looking for extensions with an empty clause" << endl;
    return;
  }
  find_extensions(u, result, c[0], 0, var_index, term_index);
}

find_start()

pair< bool, size_t > Matrix::find_start

(

)

const

Use a simple heuristic to find a good start clause.

Find a start clause that is positive/negative according to the –negative flag, and if possible also a conjecture clause. Also, indicate if there is no positive/negative clause, which means the problem is trivial.

Definition at line 51 of file Matrix.cpp.

                                           {
  bool found_positive = false;
  bool found_negative = false;
  size_t first_positive = 0;
  size_t first_negative = 0;
  bool found_candidate = false;
  size_t candidate = 0;
  size_t i = 0;
  for (bool positive : positive_clauses) {
    if (positive_clauses[i]) {
      if (!found_positive) {
        first_positive = i;
        found_positive = true;
      }
    }
    if (negative_clauses[i]) {
      if (!found_negative) {
        first_negative = i;
        found_negative = true;
      }
    }
    if (is_conjecture(i) && !found_candidate) {
      if ((params::positive_representation && positive_clauses[i]) ||
         (!params::positive_representation && negative_clauses[i])) {
            found_candidate = true;
            candidate = i;
      }
    }
    i++;
  }
  if (!(found_positive && found_negative))
    return pair<bool,size_t>(false, 0);
  if (found_candidate)
    return pair<bool, size_t>(true, candidate);
  else if (params::positive_representation)
    return pair<bool, size_t>(true, first_positive);
  else
    return pair<bool, size_t>(true, first_negative);
}

get_num_clauses()

ClauseNum Matrix::get_num_clauses ( ) const

inline

Straightforward get method.

Definition at line 227 of file Matrix.hpp.

{ return clauses.size(); }

is_conjecture()

bool Matrix::is_conjecture

(

size_t

i

)

const

Is a particular Clause a conjecture?

Parameters

i	Index of Clause to check.

Definition at line 46 of file Matrix.cpp.

                                         {
  return clause_roles[i] == "negated_conjecture" ||
         clause_roles[i] == "conjecture";
}

is_negative()

bool Matrix::is_negative ( size_t i ) const

inline

Is a particular Clause negative?.

Parameters

i	Index of Clause to check.

Definition at line 247 of file Matrix.hpp.

{ return negative_clauses[i]; }

is_positive()

bool Matrix::is_positive ( size_t i ) const

inline

Is a particular Clause positive?.

Parameters

i	Index of Clause to check.

Definition at line 241 of file Matrix.hpp.

{ return positive_clauses[i]; }

make_clauses_copy()

void Matrix::make_clauses_copy ( )

inlineprivate

Store a copy of the clauses.

Definition at line 152 of file Matrix.hpp.

                             {
      clauses_copy.clear();
      clauses_copy = clauses;
      roles_copy.clear();
      roles_copy = clause_roles;
    }

make_LaTeX()

string Matrix::make_LaTeX

(

bool

subbed = false

)

const

Make a usable LaTeX representation.

Parameters

subbed

Implement substitutions if true.

Definition at line 273 of file Matrix.cpp.

                                           {
  string s ("\\[\n\\begin{split}\n");
  s += "\\textcolor{magenta}{M} = ";
  for (const Clause& c : clauses) {
    s += "&\\,";
    s += c.make_LaTeX(subbed);
    s += "\\\\";
  }
  s += "\n\\end{split}\n\\]\n";
 
  return s;
}

move_equals_to_start()

void Matrix::move_equals_to_start

(

)

Self-explanatory.

BUT only do this to the matrix built at the start of the process, as it assumes the equality axioms are at the end of the matrix.

Definition at line 183 of file Matrix.cpp.

                                  {
  if (num_equals == 0) {
    cerr << "Why are you trying to move equality axioms - there aren't any?" << endl;
    return;
  }
  make_clauses_copy();
  clauses.clear();
  positive_clauses.clear();
  negative_clauses.clear();
  clause_roles.clear();
  size_t s2 = index.size();
  index.clear();
  index = vector<vector<MatrixPairType> >(s2, vector<MatrixPairType>());
  size_t n_clauses = clauses_copy.size();
  for (size_t i = n_clauses - num_equals; i < n_clauses; i++) {
    add_clause(clauses_copy[i], roles_copy[i]);
  }
  for (size_t i = 0; i < n_clauses - num_equals; i++) {
    add_clause(clauses_copy[i], roles_copy[i]);
  }
  clauses_copy.clear();
  roles_copy.clear();
}

operator[]()

const Clause & Matrix::operator[] ( size_t i ) const

inline

Straightforward get method.

Beware - the parameter is not checked, so behave!

Parameters

i	Index of item to get.

Definition at line 235 of file Matrix.hpp.

{ return clauses[i]; }

random_reorder()

void Matrix::random_reorder

(

)

Randomly reorder the matrix.

Definition at line 136 of file Matrix.cpp.

                            {
  vector<Clause> saved_clauses(clauses);
  vector<string> saved_clause_roles(clause_roles);
  /*
  * Find a suitably reordered set of indices.
  */
  vector<uint32_t> new_order;
  size_t s = clauses.size();
  for (size_t i = 0; i < s; i++)
    new_order.push_back(i);
  std::shuffle(new_order.begin(), new_order.end(), d);
  /*
  * Clear and rebuild as necessary.
  */
  clauses.clear();
  positive_clauses.clear();
  negative_clauses.clear();
  clause_roles.clear();
  size_t s2 = index.size();
  index.clear();
  index = vector<vector<MatrixPairType> >(s2, vector<MatrixPairType>());
  for (size_t i = 0; i < s; i++) {
    add_clause(saved_clauses[new_order[i]], saved_clause_roles[new_order[i]]);
  }
}

random_reorder_literals()

void Matrix::random_reorder_literals

(

)

Randomly reorder the literals in each clause in the matrix.

Definition at line 162 of file Matrix.cpp.

                                     {
  vector<Clause> saved_clauses(clauses);
  vector<string> saved_clause_roles(clause_roles);
  size_t s = clauses.size();
  /*
  * Clear and rebuild as necessary, reordering as you go.
  */
  clauses.clear();
  positive_clauses.clear();
  negative_clauses.clear();
  clause_roles.clear();
  size_t s2 = index.size();
  index.clear();
  index = vector<vector<MatrixPairType> >(s2, vector<MatrixPairType>());
  for (size_t i = 0; i < s; i++) {
    Clause c(saved_clauses[i]);
    c.random_reorder();
    add_clause(c, saved_clause_roles[i]);
  }
}

set_num_equals()

void Matrix::set_num_equals ( uint32_t n )

inline

Straightforward set method.

Parameters

n	Number of equality axioms.

Definition at line 259 of file Matrix.hpp.

{ num_equals = n; } 

set_num_preds()

void Matrix::set_num_preds

(

size_t

num_predicates

)

Make an empty index.

Definition at line 42 of file Matrix.cpp.

                                                {
    index = vector<vector<MatrixPairType> >((num_predicates * 2), vector<MatrixPairType>());
}

show_tptp()

void Matrix::show_tptp

(

)

const

Output in TPTP compatible format.

Definition at line 303 of file Matrix.cpp.

                             {
  size_t matrix_i = 0;
  for (const Clause& c : clauses) {
    cout << "cnf(matrix-";
    cout << std::to_string(matrix_i++);
    cout << ", plain, ";
    cout << c.to_tptp_string();
    cout << ").";
    cout << std::endl;
  }
}

sort_clauses()

template<class Comparison >

void Matrix::sort_clauses ( Comparison comparison )

inlineprivate

Template method for general sorting of clauses, which sorts roles at the same time.

ClauseComparisons.hpp contains function objects that can be used with this to implement different orderings.

Definition at line 166 of file Matrix.hpp.

                                             {
      /*
      * Combine the clauses with their roles.
      */
      vector<ClauseAndRole> cr;
      size_t s = clauses.size();
      for (size_t i = 0; i < s; i++) {
        cr.push_back(ClauseAndRole(clauses[i], clause_roles[i]));
      }
      /*
      * Sort them according to the relevant ordering.
      */
      std::sort(cr.begin(), cr.end(), comparison);
      /*
      * Split them again and re-build the index.
      */
      clauses.clear();
      positive_clauses.clear();
      negative_clauses.clear();
      clause_roles.clear();
      size_t s2 = index.size();
      index.clear();
      index = vector<vector<MatrixPairType> >(s2, vector<MatrixPairType>());
      for (size_t i = 0; i < s; i++) {
        add_clause(cr[i].first, cr[i].second);
      }
    }

sort_clauses_by_increasing_size()

void Matrix::sort_clauses_by_increasing_size ( )

inline

Self-explanatory.

Inspired by "Machine Learning Guidance for Connection Tableaux," Farber et al. 2020 although with a different measure of size and happening at a different place.

Makes use of the sort_clauses template.

Definition at line 379 of file Matrix.hpp.

                                           {
      ClauseLengthCompare comparison;
      sort_clauses<ClauseLengthCompare>(comparison);
    }

to_string()

string Matrix::to_string

(

)

const

Make a string representation.

Definition at line 250 of file Matrix.cpp.

                               {
  string result;
  colour_string::ColourString cs(params::use_colours);
  size_t i = 0;
  for (const Clause& c : clauses) {
    if (is_conjecture(i))
      result += cs("*").orange();
    else
      result += " ";
    if (positive_clauses[i])
      result += cs("+").orange();
    else if (negative_clauses[i])
      result += cs("-").orange();
    else
      result += " ";
    result += " ";
    i++;
    result += c.to_string();
    result += "\n";
  }
  return result;
}

write_to_prolog_file()

void Matrix::write_to_prolog_file

(

const path &

path_to_file

)

const

Write to a file that can be read by Prolog.

This is for proof checking.

Parameters

path_to_file

Reference to path object.

Definition at line 286 of file Matrix.cpp.

                                                                {
  std::ofstream file(path_to_file);
  size_t matrix_i = 0;
  // Nasty hack needed to stop the proof checker from printing 
  // a bunch of warnings when reading the matrix.
  file << ":- style_check(-singleton)." << std::endl;
  for (const Clause& c : clauses) {
    file << "matrix(";
    file << std::to_string(matrix_i++);
    file << ", ";
    file << c.to_prolog_string();
    file << ").";
    file << std::endl;
  }
  file.close();
}

Friends And Related Symbol Documentation

operator<<

ostream & operator<< ( ostream & out, const Matrix & m )

friend

Definition at line 315 of file Matrix.cpp.

                                                   {
    out << "Clauses in matrix:" << endl;
    out << "------------------" << endl;
    size_t i = 0;
    for (const Clause& c : m.clauses)
        out << setw(params::output_width) << i++
        << ": " << c << endl;
    vector<string> index_lits(m.index.size(), string(""));
    for (Clause c : m.clauses)
      for (size_t i = 0; i < c.size(); i++)
        index_lits[c[i].get_pred_as_index()] = c[i].get_small_lit();
    i = 0;
    out << endl << "Index: (Clause, Literal):" << endl;
    out <<         "-------------------------" << endl;
    for (vector<MatrixPairType> v : m.index) {
        out << setw(params::output_width + 20) << index_lits[i++] << ": ";
        for (MatrixPairType p : v) {
            out << "(" << p.first << ", " << p.second << ") ";
        }
        out << endl;
    }
    return out;
}

Member Data Documentation

clause_roles

vector<string> Matrix::clause_roles

private

Keep track of which clauses are conjectures etc.

This allows start clause heuristics to be applied.

Definition at line 96 of file Matrix.hpp.

clauses

vector<Clause> Matrix::clauses

private

The Matrix itself is just a set of Clauses.

Definition at line 78 of file Matrix.hpp.

clauses_copy

vector<Clause> Matrix::clauses_copy

private

It makes sense to keep a copy of the clauses if your schedule reorders multiple times.

Definition at line 106 of file Matrix.hpp.

copy_saved

bool Matrix::copy_saved

private

Remember whether you've saved a copy.

Definition at line 115 of file Matrix.hpp.

d

std::mt19937 Matrix::d

staticprivate

Randomness for random reordering.

Definition at line 127 of file Matrix.hpp.

index

vector<vector<MatrixPairType> > Matrix::index

private

We want to be able to quickly identify where in each clause a particular literal lives.

Store clause and position as pairs in a row corresponding to the literal.

Definition at line 123 of file Matrix.hpp.

negative_clauses

vector<bool> Matrix::negative_clauses

private

Keep track of which clauses are negative.

This allows start clause heuristics to be applied.

Definition at line 90 of file Matrix.hpp.

num_equals

uint32_t Matrix::num_equals

private

You need to know how many equality axioms there are in case you want to move them around.

Definition at line 101 of file Matrix.hpp.

positive_clauses

vector<bool> Matrix::positive_clauses

private

Keep track of which clauses are positive.

This allows start clause heuristics to be applied.

Definition at line 84 of file Matrix.hpp.

roles_copy

vector<string> Matrix::roles_copy

private

It makes sense to keep a copy of the roles if your schedule reorders multiple times.

Definition at line 111 of file Matrix.hpp.

---

The documentation for this class was generated from the following files:

• /Users/sbh11/Desktop/connection-prover/c++/connect++/source/Matrix.hpp
• /Users/sbh11/Desktop/connection-prover/c++/connect++/source/Matrix.cpp