


Next: Example Problem Set 3
Up: Continuous Mathematics
Previous: Example Problem Set 1
We compute the representation of some continuous function f(t)in a space spanned by an orthonormal family
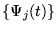 of
continuous basis functions by projecting f(t) onto them.
We express these projections in bracket notation
of
continuous basis functions by projecting f(t) onto them.
We express these projections in bracket notation
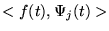 denoting
denoting
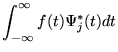 ,
where the * denotes complex conjugate;
and f(t) is assumed to be square-integrable.
,
where the * denotes complex conjugate;
and f(t) is assumed to be square-integrable.
- 1.
- Give an expression for computing f(t) if we know only its
projections
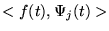 onto this set of basis
functions
onto this set of basis
functions
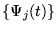 .
Explain what is happening.
.
Explain what is happening.
- 2.
- Now give an expression for computing
f(n)(t), the nth
derivative of f(t) with respect to t, in terms of the same projections
and continuous basis set. (You may assume the existence
of all derivatives.) Explain your answer.
- 3.
- Now consider a linear, time-invariant system with impulse-response
function h(t), having time-varying
input s(t) and time-varying output r(t):
In the case that the input is the complex exponential
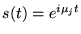 (where
(where
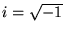 and
and 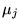 is a constant), what can you say about
the output r(t) of such a system?
is a constant), what can you say about
the output r(t) of such a system?
- 4.
- If the input s(t) has been represented in terms of a
set of complex exponentials
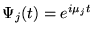 as
described at the beginning of these problems, is it possible for
different complex exponentials (not included in this set)
to appear in the output r(t) when it too is represented in terms of
complex exponentials? Justify your answer.
as
described at the beginning of these problems, is it possible for
different complex exponentials (not included in this set)
to appear in the output r(t) when it too is represented in terms of
complex exponentials? Justify your answer.



Next: Example Problem Set 3
Up: Continuous Mathematics
Previous: Example Problem Set 1
Neil Dodgson
2000-10-20
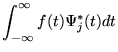 ,
where the * denotes complex conjugate;
and f(t) is assumed to be square-integrable.
,
where the * denotes complex conjugate;
and f(t) is assumed to be square-integrable.