


Next: Example Problem Set 2
Up: Continuous Mathematics
Previous: Continuous Mathematics
Many important problems in mathematical modeling and scientific
computing require the use of complex variables. Assuming
that the quantities
a, b, c, d are all reals and
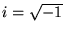 ,
resolve the following expressions, or explain the following
operations, involving complex variables
z1 = a + i b and
z2 = c + i d:
,
resolve the following expressions, or explain the following
operations, involving complex variables
z1 = a + i b and
z2 = c + i d:
- 1.
- Let
z3 = z1z2. What is the real part
of z3, and what is its imaginary part?
- 2.
- What is
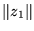 ,
the modulus of z1, and what
is
,
the modulus of z1, and what
is
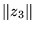 ,
the modulus of
z3=z1z2?
,
the modulus of
z3=z1z2?
- 3.
- What is
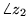 ,
the angle of complex variable z2?
,
the angle of complex variable z2?
- 4.
- Express z1 in polar complex form, not using the quantities
a or b but rather the modulus
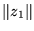 and angle
and angle
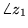 .
.
- 5.
- Suppose that z1 and z2 both have a modulus of 1.
Explain how their product
z3 = z1z2 amounts
to a rotation in the complex plane, with the aid of a diagram. Why is the
multiplication of these complex variables reduced now to
addition?
Without using the quantities
a, b, c, d, what is the value
of
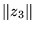 ?
?
- 6.
- Suppose that in polar complex form,
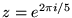 .
What
do you get if z is multiplied by itself 5 times? Give the simplest
possible answer that you can.
.
What
do you get if z is multiplied by itself 5 times? Give the simplest
possible answer that you can.
- 7.
- Consider the complex exponential function
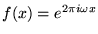 .
What function is its real part? What function is its imaginary part?
.
What function is its real part? What function is its imaginary part?
- 8.
- If the above function f(x) passes through a linear system, i.e. is
operated upon by any conceivable linear differential or integral
operator, what is the most dramatic
way in which f(x) can possibly be affected?



Next: Example Problem Set 2
Up: Continuous Mathematics
Previous: Continuous Mathematics
Neil Dodgson
2000-10-20