| |
(94) |
The antonym of rational is non-rational. Non-rational B-splines are a special case of rational B-splines, just as uniform B-splines are a special case of non-uniform B-splines. Thus, non-uniform rational B-splines encompass almost every other possible 3D shape definition. Non-uniform rational B-spline is a bit of a mouthful and so it is generally abbreviated to NURBS.
We have already learnt all about the the B-spline bit of NURBS and about the non-uniform bit. So now all we need to know is the meaning of the rational bit and we will fully(?) understand NURBS.
Rational B-splines are defined simply by applying the B-spline equation
(Equation 87) to homogeneous coordinates, rather
than normal 3D coordinates. We discussed homogeneous coordinates in
the IB course. You will remember that these are 4D
coordinates where the transformation from 4D to 3D is:
| (95) |
| (96) |
A NURBS curve is thus defined as:
We now want to see what a NURBS curve looks like in normal 3D
coordinates, so we need to apply Equation 94 to
Equation 97. In order to better explain what is
going on, we first write Equation 97 in terms of its
individual components. Equation 97 is equivalent to:
| x'(t) | = | 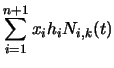 |
(98) |
| y'(t) | = | 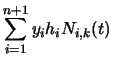 |
(99) |
| z'(t) | = | 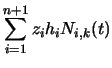 |
(100) |
| h(t) | = | 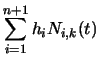 |
(101) |
| x(t) | = | x'(t)/h(t) | (102) |
| y(t) | = | y'(t)/h(t) | (103) |
| z(t) | = | z'(t)/h(t) | (104) |
So now, we need to define an additional parameter, hi, for each
control point, ![]() .
The default is to set
.
The default is to set
![]() .
This results in the denominator of
Equation 105 becoming one, and the NURBS equation
(Equation 105) therefore reducing to the
non-rational B-spline equation (Equation 87).
.
This results in the denominator of
Equation 105 becoming one, and the NURBS equation
(Equation 105) therefore reducing to the
non-rational B-spline equation (Equation 87).
Increasing hi pulls the curve closer to point ![]() .
Decreasing hi pushes the curve farther from point
.
Decreasing hi pushes the curve farther from point ![]() .
Setting hi=0 means that
.
Setting hi=0 means that ![]() has no effect on the curve at
all.
has no effect on the curve at
all.
A non-rational B-spline or a Bezier curve cannot exactly represent a
circle. An interesting exercise is to place a cubic Bezier curve's
end points at (0,1) and (1,0), with the other control points at
![]() and
and
![]() .
Now see how close this ``quarter circle'' comes
to the real quarter circle defined by
x2 + y2 = 1, i.e. what is
the value of
.
Now see how close this ``quarter circle'' comes
to the real quarter circle defined by
x2 + y2 = 1, i.e. what is
the value of ![]() for which the Bezier curve most closely matches
the quarter circle.
for which the Bezier curve most closely matches
the quarter circle.
NURBS can be used to represent circles, and all of the other conics. NURBS surfaces can be used to represent quadric surfaces. As an example, let us consider one way in which NURBS can be used to describe a true circle. Rogers and Adams cover this on pages 371-375.
Construct eight control points in a square. Let ![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() be the vertices of the
square. Let
be the vertices of the
square. Let ![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() be the midpoints of the respective sides, so that the vertices are
numbered sequentially as you proceed around the square. Finally, you
need a ninth point to join up the curve, so let
be the midpoints of the respective sides, so that the vertices are
numbered sequentially as you proceed around the square. Finally, you
need a ninth point to join up the curve, so let
![]() .
.
Use a quadratic B-spline basis function with the knot vector
[0,0,0,1,1,2,2,3,3,4,4,4]. This means that the curve will pass
through ![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() ,
and allows us to essentially treat each quarter of the
circle independently.
,
and allows us to essentially treat each quarter of the
circle independently.
We finally need to specify the homogeneous co-ordinates. As a circle
is symmetrical is should be obvious that that
![]() and
and
![]() .
As we would like the curve to pass
through the even numbered points we know that
.
As we would like the curve to pass
through the even numbered points we know that ![]() .
All we
therefore need to determine is
.
All we
therefore need to determine is ![]() ,
the value of the odd numbered
homogeneous co-ordinates.
,
the value of the odd numbered
homogeneous co-ordinates.
If ![]() then the NURBS curve will bulge out more than a
circle. If
then the NURBS curve will bulge out more than a
circle. If ![]() ,
it will bow in. This gives us limits on the
value of
,
it will bow in. This gives us limits on the
value of ![]() .
To find the exact value we take one quarter of the
NURBS curve definition:
.
To find the exact value we take one quarter of the
NURBS curve definition:
| (108) |
A NURBS surface is defined as the same two-dimensional extension to NURBS curves described in Equation 93, though obviously carried out in homogeneous co-ordinates. You can define sweeps using NURBS curves by using one NURBS curve as the sweep path, and another NURBS curve as the cross-section. You take the tensor product of the two curves. This will be described more fully in the lectures and is covered in Rogers & Adams, pages 445-456, 465-477.