Next: B-splines
Up: No Title
Previous: Ray tracing primitives
Subsections
A Bezier curve is a weighted sum of n+1 control points,
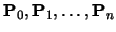 ,
where the weights
are the Bernstein polynomials:
,
where the weights
are the Bernstein polynomials:
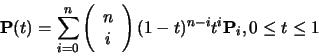 |
(74) |
The Bezier curve of order n+1 (degree n) has n+1 control
points. These are the first three orders of Bezier curve definitions.
There are several useful ways in which you can think about Bezier
curves. Here are the ones that I use.
- Linear interpolation.
- Equation 75 is obviously
a linear interpolation between two points. Equation 76 can
be rewritten as a linear interpolation between linear interpolations
between points:
![\begin{displaymath}{\bf P}(t) = (1-t)[(1-t){\bf P}_0 + t{\bf P}_1] +
t[(1-t){\bf P}_1 + t{\bf P}_2]
\end{displaymath}](img121.gif) |
(78) |
Equation 77 can be rewritten as a linear interpolation
between linear interpolations between linear interpolations between
points. This is left as an exercise for the reader.
- Weighted average.
- A Bezier curve can be seen as a weighted
average of all of its control points. Because all of the weights are
positive, and because the weights sum to one, the Bezier curve is
guaranteed to lie within the convex hull of its control points.
- Refinement of the control polygon.
- A Bezier curve can be seen
as some sort of refinement of the polygon made by connecting its
control points in order. The Bezier curve starts and ends at the two
end points and its shape is determined by the relative positions of
the n-1 other control points, although it will generally not pass
through these other control points. The tangent vectors at the start
and end of the curve pass through the end point and the immediately
adjacent point.
Rogers and Adams list the properties of the Bezier curve on
page 291.
You should note that each Bezier curve is independent of any other
Bezier curve. If we wish two Bezier curves to join with any type of
continuity, then we must explicitly position the control points of the
second curve so that they bear the appropriate relationship with the
control points in the first curve.
Any Bezier curve is infinitely differentiable within itself, and is
therefore continuous to any degree (Cn-continuous, 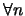 ). We
therefore only need concern ourselves with continuity across the joins
between curves. Assume that we have two Bezier curves of the same
order:
). We
therefore only need concern ourselves with continuity across the joins
between curves. Assume that we have two Bezier curves of the same
order:
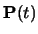 ,
defined by
,
defined by
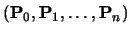 ,
and
,
and
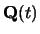 ,
defined by
,
defined by
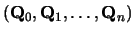 .
C0-continuity (continuity of position) can be achieved by setting
.
C0-continuity (continuity of position) can be achieved by setting
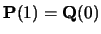 .
This gives a formula for
.
This gives a formula for 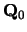 in
terms of the
in
terms of the 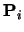 s:
s:
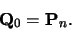 |
(79) |
Similarly for C1-continuity, we need C0-continuity and
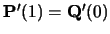 ,
giving:
,
giving:
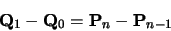 |
(80) |
Combining Equations 80 and 79 gives a
formula for 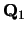 in terms of the
in terms of the 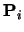 s:
s:
Continuing in this vein, we find that the requirements for
C2-continuity (i.e. C1-continuity and
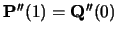 )
give:
)
give:
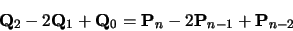 |
(83) |
Combining Equations 83, 80,
and 79 gives a formula for 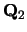 in terms of the
in terms of the
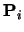 s:
s:
We learnt in the IB course that the simplest way to construct
a Bezier surface is as the tensor product of Bezier curves. A tensor product
Bezier surface of order n+1 is defined by (n+1)2 control
points. It is called a Bezier patch.
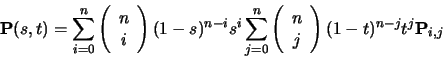 |
(86) |
You can think about this as moving the control points of one Bezier curve
along a set of Bezier curves to sweep out a surface. Continuity across
a boundary between two Bezier patches is only guaranteed if each of
the Bezier curves across the join obey the curve continuity
conditions. Again, this was covered in the IB course.



Next: B-splines
Up: No Title
Previous: Ray tracing primitives
Neil Dodgson
2000-09-25
![]() ,
where the weights
are the Bernstein polynomials:
,
where the weights
are the Bernstein polynomials:
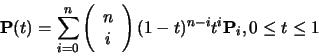
![]() ). We
therefore only need concern ourselves with continuity across the joins
between curves. Assume that we have two Bezier curves of the same
order:
). We
therefore only need concern ourselves with continuity across the joins
between curves. Assume that we have two Bezier curves of the same
order:
![]() ,
defined by
,
defined by
![]() ,
and
,
and
![]() ,
defined by
,
defined by
![]() .
C0-continuity (continuity of position) can be achieved by setting
.
C0-continuity (continuity of position) can be achieved by setting
![]() .
This gives a formula for
.
This gives a formula for ![]() in
terms of the
in
terms of the ![]() s:
s: