Part 1: Basic 3D Modelling
A: Ray tracing vs polygon scan conversion
B: Polygon mesh management & hardware PSC quirks
on to part 2...
The normal vector does not need to be specified independently of the polygon's vertices because it can be calculated from the vertices. As an example: assume a polygon has three vertices, A, B and C. The normal vector can be calculated as: n = (C-B) x (A-B).
Any three adjacent vertices in a polygon can be used to calculate the normal vector but the order in which the vertices are specified is important: it changes whether the vector points up or down relative to the polygon. In a right-handed co-ordinate system the three vertices must be specified anti-clockwise round the polygon as you look down the desired normal vector (i.e. as you look at the front side of the polygon). Note that, if there are more than three vertices in the polygon, they must all lie in the same plane, otherwise the shape will not be a polygon!
Thus, for drawing purposes, we need to know only the vertices and surface properties of the polygon. The vertices naturally give us both edge and orientation information. The surface properties are such things as the specular and diffuse colours, and details of any texture mapping which may be applied to the polygon.
The winged-edge data structure is particularly useful for handling polygon mesh data. It contains explicit links for all of the relationships between vertices, edges and polygons, thus making it easy to find, for example, which polygons are attached to a given vertex, or which polygons are adjacent to a given polygon (by traversing the edge list for the given polygon, and finding which polygon lies on the other side of each edge).
The vertex object contains the vertex's co-ordinates, a pointer to a list of all edges of which this vertex is an end-point, and a pointer to a list of all polygons of which the vertex is a vertex.
The polygon object contains (a pointer to) the polygon's surface property information, a pointer to a list of all edges which bound this polygon, and a pointer to an ordered list of all vertices of the polygon.
The edge object contains pointers to its start and end vertices, and pointers to the polygons which lie to the left and right of it.
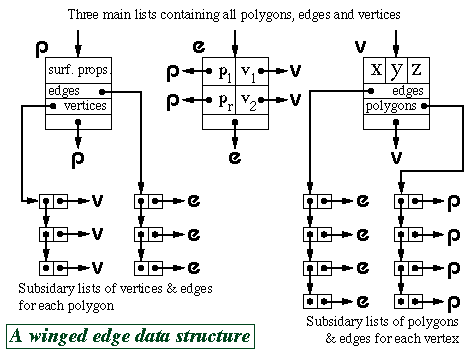
The above diagram shows just one possible implementation of a polygon mesh data structure. FvDFH section 12.5.2 describes another winged-edge data structure which contains slightly less information, and therefore requires more accesses to find certain pieces of information than the one shown above. The implementation that would be chosen depends on the needs of the particular application which is using the data structure. Another alternative would be to attach shading information to vertices rather than to polygons. This could then be used to Gouraud shade or Phong shade the polygons.
F&vD section 13.2 also contains a bit of information on polygon meshes.
In general, we will want a polygon mesh to form a manifold surface. This is where the neighbourhood of every point is topologically equivalent to a disc (except at the edges of the manifold, where it is topologically equivalent to a half disc). The principal upshot of this is that each edge in the polygon mesh can be the edge of either one or two polygons, no more and no less.
For example, assume we have triangles ABC, BCD, CDE and DEF. In standard triangle rendering, the vertices would be sent to the geometry engine in the order ABC BCD CDE DEF; each triangle's vertices being sent separately. With a triangle strip set the vertices are sent as ABCDEF; the adjacent triangles' vertices overlapping.
A triangle fan set is similar. In the four triangle case we would have triangles ABC, ACD, ADE and AEF. The vertices would again be sent just as ABCDEF. It is obviously important that the rastering engine be told whether it is drawing standard triangles or a triangle strip set or a triangle fan set.
Exercises
|
Part 1: Basic 3D Modelling
A: Ray tracing vs polygon scan conversion
B: Polygon mesh management & hardware PSC quirks
on to part 2...