Rent's Rule Estimate of Wire Length

If we know the physical area of each leaf cell we can estimate the area of each component in a heirarchic design (sum of parts plus percentage swell).

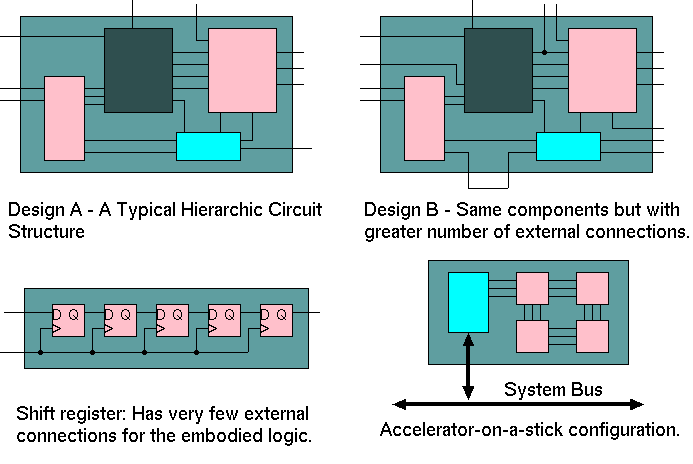
Rent's rule pertains to the organisation of computing logic, specifically the relationship between the number of external signal connections to a logic block with the number of logic gates in the logic block, and has been applied to circuits ranging from small digital circuits to mainframe computers »[Wikipedia].

Rent's rule uses a simple power-law relationship for the number of external nets to a sub-system as function of the number of logic gates in the sub-system. The figure shows three possible design styles that vary in rent coefficient.

A circuit composed of components with no local wiring between them is the other extreme possibility, with a Rent exponent of 1.0.

But the rule-of-thumb is that for most `general' subsystems a Rent exponent varying between about 0.5 and 0.7 is seen.

Circuits like the shift register can be outliers, having no increase in external connectivity regardless of length: these have a Rent exponent of 0. The same situation arises with an accelerator on-a-stick, where the degree of unfold will alter the rent exponent owing to the fixed-configuration bus port.

Generalisations of Rent's rule can model wire length distribution (with good placement). For a single level of design hierarchy, the random placement of blocks in a square of area defined by their aggregate area gives one wire length distribution (basic maths). A careful placement is used in practice, and this reduces wire length by a Rent-like factor (eg.\ by a factor of 2).

With a heirarchic design, where we have the area use of each leaf cell, even without placement, we can follow a net's trajectory up and down the hierarchy and apply Rent's Rule.

Hence we can estimate a signal's length by sampling a power law distribution whose 'maximum' is the square root of the area of the lowest-common-parent component in the hierarchy.

Illustrating Lowest Common Parent of the endpoint logic blocks. (This will always be roughly the same size for any sensible layout of a given design, so having a detailed layout like the one shown is not required).