 bits of data that are the message to be checked by the CRC can
be represented by a polynomial
bits of data that are the message to be checked by the CRC can
be represented by a polynomial 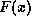 of degree
of degree  . As an example
the one octet message
. As an example
the one octet message 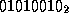 is represented by the polynomial
is represented by the polynomial
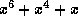 . In general, leading zero bits do not affect
. In general, leading zero bits do not affect 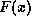 whereas
trailing zero bits each add a factor of
whereas
trailing zero bits each add a factor of  . The generating polynomial
. The generating polynomial
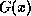 is chosen by very clever mathematicians and is essentially fixed.
The polynomial
is chosen by very clever mathematicians and is essentially fixed.
The polynomial 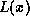 is used to represent 32 successive ones.
is used to represent 32 successive ones.
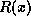 obtained from the modulo two division of
obtained from the modulo two division of 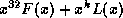 by the
generating polynomial
by the
generating polynomial 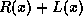 .
.
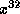 corresponds to leaving space at the end
of the message for the generated CRC. The addition of
corresponds to leaving space at the end
of the message for the generated CRC. The addition of 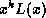 (which
is equivalent to inverting the first 32 bits of the message) precludes
erroneous addition or deletion of leading zeros. The inversion of the
CRC before sending it precludes erroneous addition of trailing zeros.
(which
is equivalent to inverting the first 32 bits of the message) precludes
erroneous addition or deletion of leading zeros. The inversion of the
CRC before sending it precludes erroneous addition of trailing zeros.
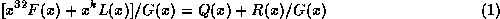
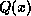 and remainder
and remainder 
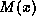 is
is 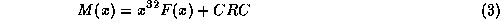
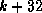 . We consider:
. We consider:
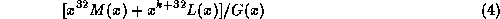
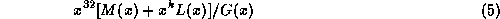
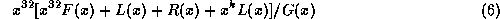
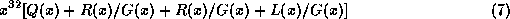

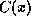 for all messages
for all messages