This process is performed in a doubly-dimensionless polar coordinate system that is invariant to the size of the iris (and hence invariant to the imaging distance and the optical magnification factor), and also invariant to the dilation diameter of the pupil within the iris.
The demodulating wavelets are parameterized with four degrees-of-freedom: size, orientation, and two positional coordinates. They span several octaves in size, in order to extract iris structure at many different scales of analysis. Because the information extracted from the iris is inherently described in terms of phase, it is insensitive to contrast, camera gain, and illumination level (unlike correlation methods). The phase description is very compact, requiring only 256 bytes to represent each iris pattern, plus control bytes that exclude artifacts such as eyelashes or reflections or data that is unstable or weak. The 2D Gabor wavelets are optimal encoders under the Heisenberg-Weyl uncertainty relation for extraction of information in conjoint spatial - spectral representations.
The recognition of irises by their IrisCodes is based upon the failure of a test of statistical independence. Any given IrisCode is statistically guaranteed to pass a test of independence against any IrisCode computed from a different eye; but it will uniquely fail this same test against the eye from which it was computed. Thus the key to iris recognition is the failure of a test of statistical independence.
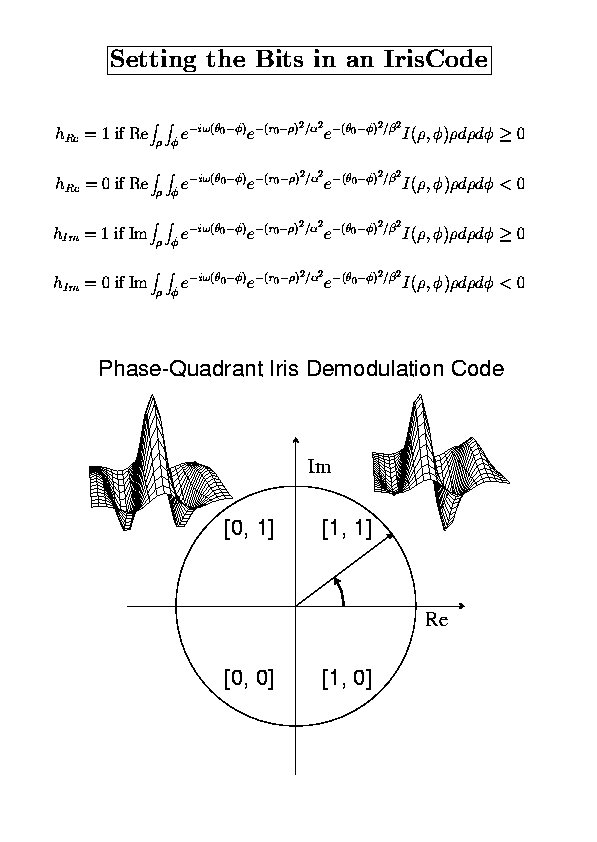
The equations and the wavelet phasor diagram below summarize the pattern encoding process. Using a Boolean XOR similarity metric on the phasor bit strings generates similarity scores among different IrisCodes that are binomially-distributed and that therefore have tails that attenuate extremely rapidly. More detailed information about the complex-valued 2D Gabor encoding wavelets, about the test of statistical independence, and the table of False Match probabilities generated by IrisCodes, can be found in the published papers cited in the References at the bottom of this page or elsewhere on this website.
