 |
An input signal is converted from some continuosly varying physical value (e.g. pressure in air, or frequency or wavelength of light), by some electro-mechanical device into a continuously varying electrical signal. This signal has a range of amplitude, and a range of frequencies that can present. This continuously varying electrical signal can then be converted to a sequence of digital values, called samples, by some analog to digital conversion circuit. Figure 4.2 illustrates this process.
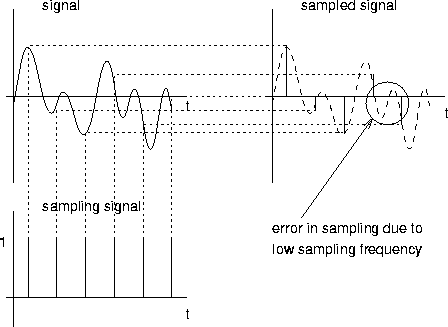
There are two factors which determine the accuracy with which the digital sequence of values captures the original continuous signal: the maximum rate at which we sample, and the number of bits used in each sample. This latter value is known as the quanisation level, and is illustrated in figure 4.3.
The raw (un-compressed) digital data rate associated with a signal then is simply the sample rate times the number of bits per sample. To capture all possible frequencies in the original signal, Nyquist's theorem shows that the digital rate must be twice the highest frequency component in the continuous signal. However, it is often not necessary to capture all frequencies in the original signal - for example, voice is comprehensible with a much smaller range of frequencies than we can actually hear. When the sample rate is much lower than the highest frequency in the continuosu signal, a band-pass filter which only allows frequencies in the range actually needed, is usally put before the sampling circuit. This avoids possible ambiguous samples (``aliases'').