The bouncing ball problem solved by Forbus' ``FROB'' involves more complex two dimensional reasoning, because there are two degrees of freedom in the ball's motion. FROB represented the problem in two different forms: the ``metric diagram'' was a geometric description of the scene, which was essentially the formatted input to the qualitative reasoning program. From the metric diagram, the system computed the ``place vocabulary'', which is the set of possible states for the moving ball, together with information about possible transitions between those states.
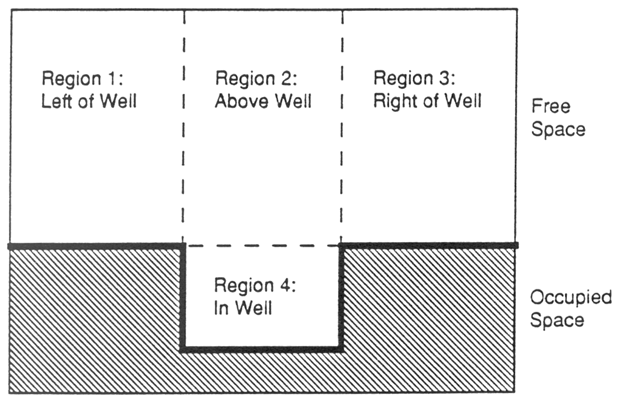
FROB divided the free space in the metric diagram into qualitatively distinct regions by extending discontinuities in the free space boundaries. This means that the prescence of a ``well'', as shown in Figure 3.1, results in the division of the otherwise uniform free space into four regions - in the well, above the well, to the left of the well, and to the right of the well.
The spatial regions in the divided metric diagram correspond directly to possible qualitative states (actually temporal locations bounded by time interval and spatial position) in the motion of the ball. From any one region, there are a finite number of other regions that the ball can move into (at most eight, including diagonals); these possible motions are represented as possible state transitions. Forbus calls this representation the ``place vocabulary''.
The division into regions from the metric diagram is always carried out along vertical and horizontal lines constructed through boundary discontinuities. The vertical direction is defined with reference to gravity, and the horizontal is perpendicular to gravitational acceleration. The effect of this is to include implicit information about gravitational acceleration and potential energy in the scene representation - speed of motion is constant in the horizontal direction, and acceleration is constant in the vertical.
The current state of the moving ball was described in terms of location (a ``place'' in the place vocabulary), and direction of motion. The next state could be determined from this information, since the place vocabulary included information about how individual places are connected to other places in each direction. The program could then derive an envisionment of possible future states, given the current state, together with the place vocabulary.
A later paper by Forbus [For82] discusses the application of his qualitative process theory to the bouncing ball problem, with motion being described as an ``influence'' on the ``position quantity'' associated with an object. Acceleration and energy are also treated as quantities which are influenced by processes. The implemented example which he describes involves one dimensional motion of a block and spring - a classic example of energy conversion. He does not suggest a definite approach for extending the energy conversion of this example to the two dimensional case of the bouncing ball, but in a more recent paper gives the opinion that ``quantity spaces don't work in more than one dimension'' [FNF87].
The approach to qualitative two dimensional reasoning which I have developed can use a quantity space technique to describe two dimensional motion and position - in terms of proximity relationships between objects. This technique is described in chapter 4.