In a space filling representation, an area of space (either the whole workspace, the visual field, or simply the locality of an operation) is partitioned into regions, which are classified as either occupied or unoccupied. An object is represented in the system simply as a collection of occupied regions. The spaces between objects are represented as explicitly as the objects themselves, and can be analysed by considering the collection of unoccupied regions.
The technique used in the Edinburgh assembly project described in the previous section is typical of the most primitive form of space-filling representation. In this system the basic units of space in the representation correspond exactly to pixels in the robot's visual field. The Edinburgh system made two dimensional images using an overhead camera. The two dimensional outline of an object lying on the table was then matched against a library of outlines for all parts. The identification of protrusions from the pile, and outline shape matching could both be carried out using a simple copy of the visual image as the internal representation. This copy was a pixel map with bits of an array set where there were light areas in the image.
The same simple representation was used in this project as the basis for visually guided arm movements. Each stored object representation had associated with it a point by which the object could be grasped, and once the identity and position of the object had been established relative to the camera (which was in a fixed position), the arm could be guided directly to the grasp point.
This hand-eye system is versatile enough to operate in many industrial environments, but the simple representation of shape results in several limitations. One limitation is that shape matching is carried out on the whole object, and where an object is partially obscured, the system cannot recognise it. The practical solution to this problem involved using the robot arm to scatter piles of objects which obscured each other; this would not be an acceptable technique in a lightbulb assembly plant! A further limitation is the restriction to parts that are adequately described by a two dimensional view.
The Edinburgh system was limited to recognising shapes that have unique outlines when lying flat on a table; it is possible, however, to use the same simple level of visual shape encoding, with more sophisticated indexing, to obtain a more complex description of three dimensional shape. The simplest way of doing this is to store outlines of an object when viewed from different angles. Grossman and Blasgen developed such a system for identifying objects, which was not limited to flat parts [GB75]. Complex parts were vibrated in a tray into one of a few stable orientations. The vision system was then able to test the image of a part in the tray for all known orientations.
The representation of the object in this case consisted of a collection of pixel maps of the possible two dimensional projections of the part in each stable orientation. Although this system was able to identify three dimensional parts more accurately and reliably than a simple overhead view, the resulting collection of projections was really only useful for part identification - a robot would require more information about the underlying part structure to plan manipulation.
A limitation of both of the above systems is that the world representation contains only the shapes that are in the visual field of the robot. Space filling representations can be made more powerful by representing the whole of the robot's workspace, rather than just its visual field. This representation must be less dependent on sensing hardware, since it cannot make direct use of image pixels.
The extension of space filling representation to the whole workspace can also involve an extended number of dimensions in the representation. If the workspace representation is not restricted to construction from the information in a single image, it can include three dimensions. Three dimensional space filling divides the workspace into regions using a three-dimensional grid, where the elements of the grid are occupied or unoccupied ``voxels''.
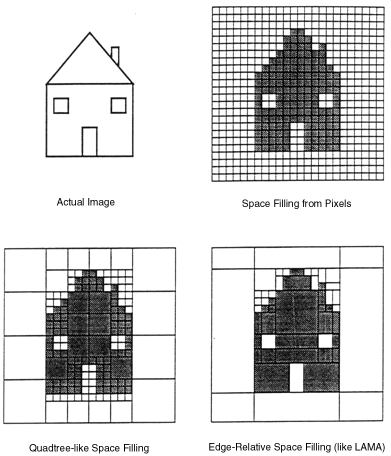
Space filling representations (whether two dimensional or three dimensional) can be made more compact and memory efficient by using schemes to describe contiguous chunks of either occupied or unoccupied space. One simple method is that of ``quadtrees'' (or ``octrees'' in the three dimensional case), which partitions the workspace using the following algorithm: The workspace is divided into quadrants (or octants). If a quadrant is homogeneously filled or empty, it is not subdivided any further. A non-homogeneous quadrant is itself divided into quadrants, and the process is repeated. This subdivision can then be carried out to any level of detail.
Lozano-Pérez's original LAMA task-level programming system [LP76] makes use of a still more sophisticated space filling approach for representing the overall workspace. This does not divide the workspace into arbitrary quadrants, but into object-specific domains at the boundaries of objects. This method can achieve improvements in accuracy, because the edges of objects are located precisely, instead of being represented at the nearest line of area units. It also involves less memory usage than the quadtree method, because the number of space divisions increases only with the number of objects (or edges), rather than with resolution accuracy. The method is, however, more computationally complex.
Figure 2.1 illustrates the various space filling methods, as
used to describe a simple scene at low resolution.
There are two very significant limitations to the space filling techniques. The first of these is that the level of accuracy which can be achieved in describing the object boundary is limited to the size of the smallest unit region. An n-times increase in accuracy therefore results in a 2n increase in memory usage for a two dimensional pixel-based system, and a larger relative increase for a quadtree system.
The second limitation is that straight-sided objects only appear to have simple boundaries if those boundaries are aligned to the grid along which the representation space is divided. The representation of an object with edges which are not aligned to the grid axes results in aliasing of the edges (this can be seen in the diagonal lines of the example). The efficiency of using regions which fit the object boundaries is also greatly reduced in this case, because it is impossible to subdivide the workspace orthogonally to fit edges. This is noted by Lozano-Perez as a weakness of the method used in his LAMA system.
The main advantage of space filling representations has been the simplicity with which they can be constructed, with the simplest case (pixel-size regions) requiring no processing at all to derive the shape representation from image data. For this reason, they are still used in industrial tasks involving simple shape matching, or location of a single workpiece within the robot workspace. (An example is the detection of a workpiece randomly located on a conveyor belt, which must be visually located so that it can be picked up by a robot arm). Where more complex reasoning is to be carried out, space filling representations soon become impractical.
A secondary advantage of space filling representations arises from the fact that empty space is explicitly represented. This is useful in path planning problems, where empty space of sufficient size for the robot arm to move through can be found directly by searching the scene representation.