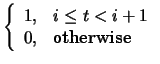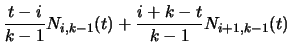Next: Rational B-splines
Up: No Title
Previous: Bezier curves
Subsections
B-splines are a more general type of curve than Bezier curves. In a
B-spline each control point is associated with a basis function.
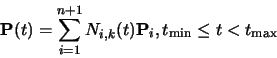 |
(87) |
There are n + 1 control points,
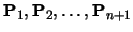 .
The Ni,k basis functions are of order k(degree k-1). k must be at least 2 (linear), and can be no more
than n+1 (the number of control points). The important point here is
that the order of the curve (linear, quadratic, cubic,...) is
therefore not dependent on the number of control points (which it is
for Bezier curves, where k must always equal n+1).
.
The Ni,k basis functions are of order k(degree k-1). k must be at least 2 (linear), and can be no more
than n+1 (the number of control points). The important point here is
that the order of the curve (linear, quadratic, cubic,...) is
therefore not dependent on the number of control points (which it is
for Bezier curves, where k must always equal n+1).
Equation 87 defines a piecewise continuous
function. A knot vector,
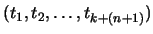 ,
must
be specified. This determines the values of t at which the pieces of
curve join, like knots joining bits of string. It is necessary that:
,
must
be specified. This determines the values of t at which the pieces of
curve join, like knots joining bits of string. It is necessary that:
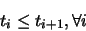 |
(88) |
The Ni,k depend only on the value of k and the values in
the knot vector. N is defined recursively as:
| Ni,1(t) |
= |
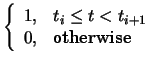 |
|
| Ni,k(t) |
= |
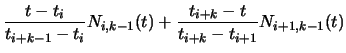 |
(89) |
This is essentially a modified version of the idea of taking linear
interpolations of linear interpolations of linear interpolations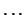 n
n
At this point it would be instructive for you to work out N1,1,
N2,1, N3,1, N1,2, N2,2, N1,3 for the knot
vector (0,2,3,6). It helps if you draw the graphs for these
functions.
There are several things that you should note about these
equations. Each
Ni,k(t) depends only on the k+1 knot values
from ti to ti+k.
Ni,k(t)=0 for t < ti or
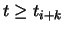 so
so
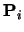 only influences the curve for
only influences the curve for
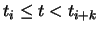 .
Formally,
.
Formally,
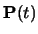 is a polynomial of order k (degree
k-1) on each interval
is a polynomial of order k (degree
k-1) on each interval
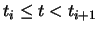 .
Across the knots
.
Across the knots
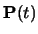 is Ck-2-continuous.
is Ck-2-continuous.
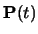 is, of course,
continuous in all its derivatives between the knots.
is, of course,
continuous in all its derivatives between the knots.
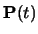 is
validly defined for
is
validly defined for
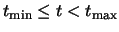 where
where
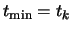 and
and
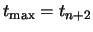 .
Even more properties of B-splines are
described in Rogers and Adams pp. 306-7.
.
Even more properties of B-splines are
described in Rogers and Adams pp. 306-7.
The above explanation shows that the knot vector is very
important. The knot vector can, by its definition, be any sequence of
numbers provided that each one is greater than or equal to the
preceding one. Some types of knot vector are more useful than
others. Knot vectors are generally placed into one of three
categories: uniform, open uniform, and non-uniform.
- Uniform.
- These are knot vectors for which
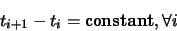 |
(90) |
For example:
- Open Uniform.
- These are uniform knot vectors which have kequal knot values at each end:
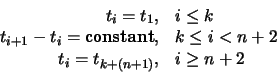 |
(91) |
For example:
- Non-uniform.
- This is the general case, the only constraint
being the standard
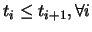 (Equations 88). For example:
(Equations 88). For example:
The shapes of the Ni,k basis functions are determined entirely by
the relative spacing between the knots. Scaling
(
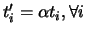 )
or translating (
)
or translating (
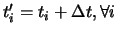 )
the knot vector has no effect on the shapes of the
Ni,k.
)
the knot vector has no effect on the shapes of the
Ni,k.
The above gives a description of the various types of knot vector but
it doesn't really give you any insight into how the knot vector
determines the shape of the curve. The following subsections look at
the different types of knot vector in more detail. However, the best
way to get to feel for these is to derive and draw the basis functions
yourself.
For simplicity, let ti = i (this is allowable given that the
scaling or translating the knot vector has no effect on the shapes of
the Ni,k). The knot vector thus becomes
![$[1,2,3,\ldots,k+(n+1)]$](img164.gif) and
Equation 89 simplifies to:
and
Equation 89 simplifies to:
| Ni,1(t) |
= |
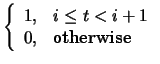 |
|
| Ni,k(t) |
= |
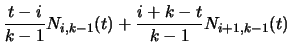 |
(92) |
You should be easily able to graph the first few of these for
yourself.
The principle thing to note about the uniform basis functions is that,
for a given order k, the basis functions are simply shifted versions
of one another.
With a uniform B-spline, you obviously cannot change the basis
functions (they are fixed because all the knots are
equispaced). However you can alter the shape of the curve by modifying
a number of things:
- Moving control points.
- Moving the control points obviously
changes the shape of the curve.
- Multiple control points.
- Sticking two adjacent control points on
top of one another causes the curve to pass closer to that
point. Stick enough adjacent control points on top of one another and
you can make the curve pass through that point.
- Order.
- Increasing the order k increases the continuity of the
curve at the knots, increases the smoothness of the curve, and tends
to move the curve farther from its defining polygon.
- Joining the ends.
- You can join the ends of the curve to make a
closed loop. Say you have M points,
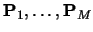 .
You want a closed B-spline defined by
these points. For a given order, k, you will need M+(k-1) control
points (repeating the first k-1 points):
.
You want a closed B-spline defined by
these points. For a given order, k, you will need M+(k-1) control
points (repeating the first k-1 points):
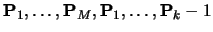 .
Your
knot vector will thus have M+2k-1 uniformly spaced knots.
.
Your
knot vector will thus have M+2k-1 uniformly spaced knots.
The previous section intimated that uniform B-splines can be used to
describe closed curves: all you have to do is join the ends as
described above. If you do not want a closed curve, and you use a
uniform knot vector, you find that you need to specify control points
at each end of the curve which the curve doesn't go near.
If you wish your B-spline to start and end at your first and last
control points then you need an open uniform knot vector. The only
difference between this and the uniform knot vector being that the
open uniform version has k equal knots at each end.
An order k open uniform B-spline with n+1=k points is the Bezier
curve of order k. It would be a useful exercise for you to prove
this for k=3. For ease of calculation take the knot vector to be
[0,0,0,1,1,1].
It may help, at this stage, to compare a particular uniform and an
equivalent open uniform knot vector.
This is a uniform knot vector for n+1=7, k=3:
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
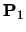 |
|
|
|
|
|
|
|
|
|
|
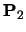 |
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
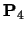 |
|
|
|
|
|
|
|
|
|
|
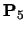 |
|
|
|
|
|
|
|
|
|
|
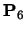 |
|
|
|
|
|
|
|
|
|
|
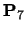 |
|
|
|
|
|
|
|
|
|
|
| overall |
|
|
|
|
|
|
|
|
|
|
The lines show the range of t over which each 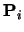 is
defined. The B-spline itself (the overall line in the diagram) is
defined over the range
is
defined. The B-spline itself (the overall line in the diagram) is
defined over the range
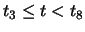 ,
i.e. over the range
,
i.e. over the range
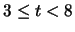 .
.
By comparison an open uniform knot vector for n+1=7, k=3 is:
| |
1 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
6 |
6 |
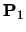 |
|
|
|
|
|
|
|
|
|
|
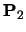 |
|
|
|
|
|
|
|
|
|
|
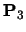 |
|
|
|
|
|
|
|
|
|
|
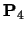 |
|
|
|
|
|
|
|
|
|
|
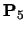 |
|
|
|
|
|
|
|
|
|
|
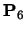 |
|
|
|
|
|
|
|
|
|
|
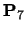 |
|
|
|
|
|
|
|
|
|
|
| overall |
|
|
|
|
|
|
|
|
|
|
The B-spline itself is defined over the range
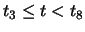 ,
i.e. over the range
,
i.e. over the range
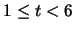 .
By the definition of a open
uniform knot vector t3=t1 and
t8=t10 and so an open uniform
B-spline is defined over the full range of t from t1 to
tk+n+1.
.
By the definition of a open
uniform knot vector t3=t1 and
t8=t10 and so an open uniform
B-spline is defined over the full range of t from t1 to
tk+n+1.
Any B-spline whose knot vector is neither uniform nor open uniform is
non-uniform. Non-uniform knot vectors allow any spacing of the knots,
including multiple knots (adjacent knots with the same value). We need
to know how this non-uniform spacing affects the basis functions in
order to understand where non-uniform knot vectors could be useful. It
transpires that there are only three cases of any interest: (1)
multiple knots (adjacent knots equal); (2) adjacent knots more closely
spaced than the next knot in the vector; and (3) adjacent knots less
closely spaced than the next knot in the vector. Obviously, case (3)
is simply case (2) turned the other way round.
- Multiple knots.
- A multiple knot reduces the degree of
continuity at that knot value. Across a normal knot the continuity is
Ck-2. Each extra knot with the same value reduces continuity at
that value by one. This is the only way to reduce the continuity of
the curve at the knot values. If there are k-1 (or more) equal knots
then you get a discontinuity in the curve.
- Close knots.
- As two knots' values get closer together, relative
to the spacing of the other knots, the curve moves closer to the
related control point.
- Distant knots.
- As two knots' values get further apart, relative
to the spacing of the other knots, the curve moves further away from
the related control point.
Standard procedure is to use uniform or open uniform B-splines unless
there is a very good reason not to do so. Moving two knots closer
together tends to move the curve only slightly and so there is usually
little point in doing it. This leads to the conclusion that the main
use of non-uniform B-splines is to allow for multiple knots, which
adjust the continuity of the curve at the knot values.
However, non-uniform B-splines are the general form of the B-spline
because they incorporate open uniform and uniform B-splines as special
cases. Thus we will talk about non-uniform B-splines when we
mean the general case, incorporating both uniform and open uniform.
- Move the control points.
- Add or remove control points.
- Use multiple control points.
- Change the order, k.
- Change the type of knot vector.
- Change the relative spacing of the knots.
- Use multiple knot values in the knot vector.
If there are no pressing reasons for doing otherwise, your B-spline
should be defined as follows:
- k=4 (cubic);
- no multiple control points;
- uniform (for a closed curve) or open uniform (for an open curve)
knot vector.
We generalise from B-spline curves to B-spline surfaces in the same
way as we did for Bezier patches. Take a tensor product of two
versions of Equation 87.
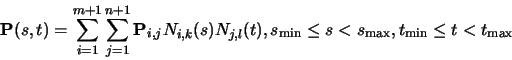 |
(93) |
where it is usual for the patch to have the same order (i.e. k=l) in
both directions.



Next: Rational B-splines
Up: No Title
Previous: Bezier curves
Neil Dodgson
2000-09-25
![]() ,
must
be specified. This determines the values of t at which the pieces of
curve join, like knots joining bits of string. It is necessary that:
,
must
be specified. This determines the values of t at which the pieces of
curve join, like knots joining bits of string. It is necessary that:
![]() so
so
![]() only influences the curve for
only influences the curve for
![]() .
Formally,
.
Formally,
![]() is a polynomial of order k (degree
k-1) on each interval
is a polynomial of order k (degree
k-1) on each interval
![]() .
Across the knots
.
Across the knots
![]() is Ck-2-continuous.
is Ck-2-continuous.
![]() is, of course,
continuous in all its derivatives between the knots.
is, of course,
continuous in all its derivatives between the knots.
![]() is
validly defined for
is
validly defined for
![]() where
where
![]() and
and
![]() .
Even more properties of B-splines are
described in Rogers and Adams pp. 306-7.
.
Even more properties of B-splines are
described in Rogers and Adams pp. 306-7.
![\begin{displaymath}\begin{array}{l}
\ [1,2,3,4,5,6,7,8]\\
\ [0,1,2,3,4,5]\\
\ ...
...25,0.5,0.75,1.0]\\
\ [-2.5,-1.4,-0.3,0.8,1.9,3 .0]
\end{array}\end{displaymath}](img157.gif)
![\begin{displaymath}\begin{array}{ll}
\ [0,0,0,0,1,2,3,4,4,4,4] & (k=4)\\
\ [1,1...
....1,0.1,0.1,0.1,0.3,0.5,0.7,0.7,0.7,0.7,0.7] & (k=5)
\end{array}\end{displaymath}](img159.gif)
![\begin{displaymath}\begin{array}{l}
\ [1,3,7,22,23,23,49,50,50] \\
\ [1,1,1,2,2...
...,6,6,7,7,7] \\
\ [0.2,0.7,0.7,0.7,1.2,1.2,2.9,3.6]
\end{array}\end{displaymath}](img161.gif)
![]() )
or translating (
)
or translating (
![]() )
the knot vector has no effect on the shapes of the
Ni,k.
)
the knot vector has no effect on the shapes of the
Ni,k.
![]() and
Equation 89 simplifies to:
and
Equation 89 simplifies to: