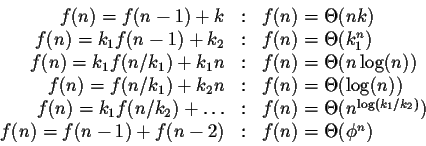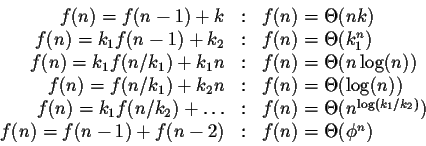
When analysing algorithms one will often end up with a proof by induction
that shows that the method described does indeed always solve the problem
it was supposed to. Quite frequently this proof can be extended to
yield a way of estimating the costs involved. Look back to the
Tower of Hanoi example, and now we know that given a tower of n discs
it can be moved from one peg to another, consider how many elementary
moves will be used if we follow the recipe implicit in the inductive
proof. To do this start by introducing a name for the cost, say
M(n) for the number of steps to move n discs. Then from the
base case of the induction we have M(1) = 1. The induction step
shows that success is possible by a route which gives
This course will not have either the time or inclination to show you all
the clever ways there are of solving recurrence formula, and
instead just provides a cook-book listing some of the more commonly
arising ones and indicating their solutions. Symbols with names
like k stand for constants, and will sometimes need to have values
larger than 0 or 1 for the results quoted to be valid.