Advanced Graphics

Lecture 2 Index
...back to lecture 1
Part A: Conics, quadrics, and superquadrics
Part B: Generative models
Part C: Converting primitives to polygons
on to lecture 3...

2B) Generative models

Sweeps

Surfaces of revolution are covered in R&A section 6-2. Sweeps are covered in R&A section 6-3 and FvDFH section 12.4.

Extrusion

Surface of revolution

Revolution or extrusion?

Generalised Cylinders

• Cross section
  Some two dimensional shape that is to be swept along the sweep path. This is the cross section of the "cylinder". It does not have to be circular. At right are two generalised cylinders, one with a circular cross-section, one with a polygonal cross-section.
  
• Sweep path
  The path along which the two dimensional cross section is swept to produce the three dimensional shape. It may be any curve. At right we see two views of the same generalised cylinder: a polygonal cross-section is swept along a convoluted path.
  
• Twist
  How the cross section twists (rotates) as it moves along the sweep path. The default would be to have no twist at all. At right is a generalised cylinder with and without some twist.
  
• Scale
  
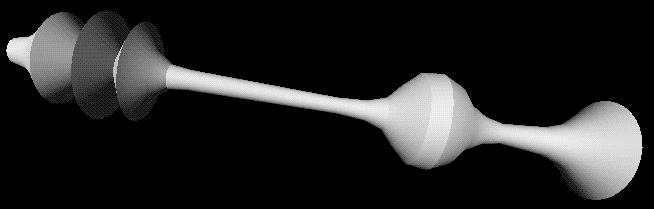
  How the cross section scales (changes size) as it moves along the sweep path. The default would be to have it stay the same size along the whole path. Above are a cylinder, and the same cylinder with different scales along its length.
  
• Normal vector direction
  The normal vector of the 2D cross section will usually point along the sweep path at each point. Changing this will change the nature of the generalised cylinder. See R&A Figure 6-17 for an example.

You may be able to think of parameters, other than those in the list above, which you could modify to make an even more generalised cylinder.

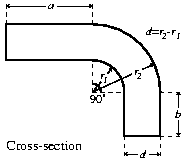
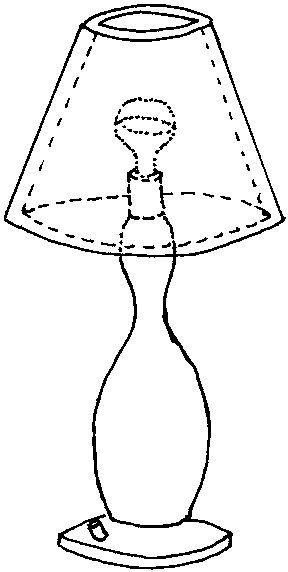
Exercises [1998/7/12] Show how the following object can be represented as a swept object. Use the following different methods of specifying a geometrical model for this picture (assuming it's a three dimensional model and not a line drawing). Come as close as you can to the original for any of the methods, and describe the difficulties in using a particular method for this model. Extrusions Surfaces of revolution Sweeps Generalized cylinders For each of the following categories list five real-world objects which could be represented by the primitives in the category. The ray-tracing primitives in Lecture 1C Extrusions Surfaces of revolution Generalized cylinders A flume (water tunnel) at a swimming complex is modeled as a circle swept along a particular path. The designers also want to model the volume swept out by a person traveling down the flume. (We can approximate the cross-section of a person with something roughly elliptical and we'll assume the `virtual' person doesn't move legs or arms while hurtling along.) Explain why a standard `sweep' is insufficient to do this and explain what form of generative model would be needed to model the volume swept out by a person traveling down the flume.

Lecture 2 Index
...back to lecture 1
Part A: Conics, quadrics, and superquadrics
Part B: Generative models
Part C: Converting primitives to polygons
on to lecture 3...