Affine transformations (Zuo, Liang et al).
A number of restricted mathematical systems have useful results in terms of decidibility of certain propositions. A restriction might be that expressions only multiply where one operand is a constant and a property might be that an expression always lies within a certain intersection of n-dimensional planes.
There is a vast literature regarding integer linear inequalities (linear programming) that can be combined with significant results from Presburger (Preburger Arithmetic) and Mine (The Octagon Domain) as a basis for optimising memory access patterns within HLS.
We seek transformations that:
1. compact provably sparse access patterns into packed form or
2. where array read subscripts can be partitioned into provably disjoint sets that can be served in parallel by different memories, or
3. where data dependencies are sufficiently determined that thread-future reads can be started at the earliest point after the supporting writes have been made so as to meet all read-after-write data dependencies.

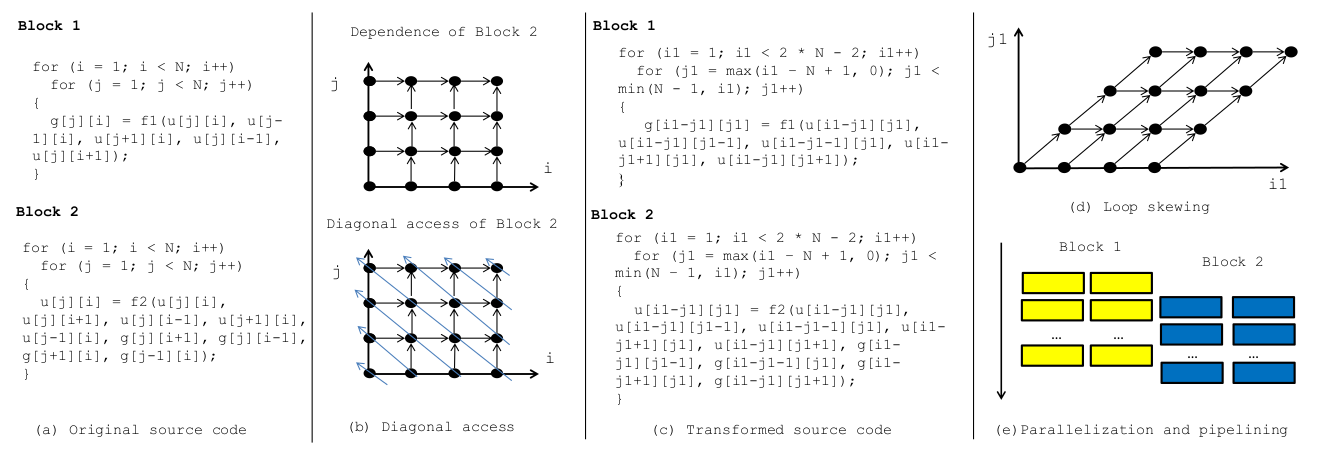
A set of nested loops where the bounds of inner loops depend on linear combinations of surrounding loop (aka induction) variables defines a polyhedral space or polytope. This space is scanned by the vector consisting of the induction variables.
Under polyhedral mapping, the loop nesting order may be changed and affine transformations are applied to many of the loop variables with the aim of exposing parallelism and/or re-packing array subscripts to use less overall memory.
In the example, both the inner and outer loop bounds are transformed.
The skewing of block 1 enables it to be parallelised with computable data dependencies. The following block, that runs on its output, can be run in parallel after an appropriately delayed start.
For big data, at least one of the loop bounds is commonly an iteration over a file streamed from secondary storage.
(The field of automatic parallelisation of nested for loops on arrays has been greatly studied over recent decades for SIMD and systolic array synthesis ...)
Q. Does the following have loop interference ?
for (i=0; i<N; i++) A[i] := (A[i] + A[N-1-i])/2A. Yes, at first glance, but we can recode it as two independent loops. (`Loop Splitting for Efficient Pipelining in High-Level Synthesis' by J Liu, J Wickerson, G Constantinides.) ``In reality, there are only dependencies from the first N/2 iterations into the last N/2, so we can execute this loop as a sequence of two fully parallel loops (from 0...N/2 and from N/2+1...N). The characterization of this dependence, the analysis of parallelism, and the transformation of the code can be done in terms of the instance-wise information provided by any polyhedral framework.''
Q. Does the following have loop body inter-dependencies ?
for (i=0; i<N; i++) A[2*i] = A[i] + 0.5f;A. Yes, but can we transform it somehow?
| 28: (C) 2012-18, DJ Greaves, University of Cambridge, Computer Laboratory. |