 |
Richard Clayton and Mike Bond
University of Cambridge, Computer Laboratory, Gates Building, JJ Thompson Avenue, Cambridge CB3 0FD, United Kingdom{ richard.clayton, mike.bond }@cl.cam.ac.uk
Abstract. This paper describes the authors' experiences attacking the IBM 4758 CCA, used in retail banking to protect the ATM infrastructure. One of the authors had previously proposed a theoretical attack to extract DES keys from the system, but it failed to take account of real-world banking security practice. We developed a practical scheme that collected the necessary data in a single 10-minute session. Risk of discovery by intrusion detection systems made it necessary to complete the key "cracking" part of the attack within a few days, so a hardware DES cracker was implemented on a US$995 off-the-shelf FPGA development board. This gave a 20-fold increase in key testing speed over the use of a standard 800 MHz PC. The attack was not only successful in its aims, but also shed new light on the protocol vulnerabilities being exploited. In addition, the FPGA development led to a fresh way of demonstrating the non-randomness of some of the DES S-boxes and indicated when pipelining can be a more effective technique than replication of processing blocks. The wide range of insights we obtained demonstrates that there can be significant value in implementing attacks "for real".
The IBM 4758 is a "cryptoprocessor" or "security module" -- a tamper-resistant coprocessor that runs software providing cryptographic and security related services. Its API is designed to protect the confidentiality and integrity of data while still permitting access according to a configurable usage policy. Cryptoprocessors are commonly used in financial environments to protect ATM (cash machine) infrastructures, process customer Personal Identification Numbers (PINs), and secure transaction streams between banks. Other applications of cryptoprocessors include the protection of credit dispensing networks for prepayment electricity meters, and governing access to keys at certification authorities.
In [2] one of the authors of this paper described a number of flaws in the Common Cryptographic Architecture (CCA) -- the default financial software for the IBM 4758. We set out to implement an actual attack on a 4758 in a simulated banking environment, combining these flaws to extract valuable key material. In particular, we wished to demonstrate the extraction of a "PIN derivation key", a Triple DES (3DES) key which can be used to calculate a customer's PIN from the account number embossed on the front of their card. By creating fake cards with real account numbers, an attacker could then use the calculated PINs to plunder ATMs of their choice, anywhere in the country.
During this process, it became clear that there is far more to implementing a practical attack than meets the eye, and we had to make substantial modifications to the scheme and create new technology in order to get the job done. As a direct result of this work, IBM have released a new version of the CCA [12] containing multiple modifications to the API to defeat each technique used, and so the attack we describe can no longer be mounted.
Section 2 summarises the theory behind the building blocks of the attack, and section 3 describes why the banking environment and procedural controls make successful application of these building blocks a difficult task. Section 4 describes the extensions made to satisfy the requirements from section 3 -- in particular, the attack was restructured to collect all necessary data within a single, very quick, period of access to the 4758. Section 5 covers the design and implementation of an FPGA based DES cracker to provide the necessary brute force attack performance. This provided some unexpected insights into DES and key cracker design generally. Section 6 presents brief results from test runs, and finally, conclusions are drawn in section 7.
In his earlier paper [2], Bond identifies a number of weaknesses in the CCA, which he termed "building blocks".
The CCA keys are typically DES or 3DES keys, and are stored by encryption under a master key. When keys are to be transferred between banks, they are encrypted with a key-encrypting key (KEK) instead of the master key. As a KEK is the highest level of key shared between banks, there is no option but to transfer the KEK itself in plaintext. The standard procedure is to split it into three parts using XOR, and transfer each part with a separate courier. At the destination, three "security officers" enter the key parts into the cryptoprocessor, which recombines them into the original key. This procedure leads to a significant security problem: although the security officers must all collude to discover the key value, just one of them could modify the final key at will by changing the value of their single key part. In fact, unknown key parts can be generated which simulate the presence of other officers and so the control that a single corrupt security officer has over their own key part is enough to allow the CCA software to be attacked.
The CCA software does not place restrictions on key generation, so it is easy to create a large number of unknown DES keys. A particular test pattern can be encrypted under each of these keys to create a set of test vectors. A brute force attack can then be used to attack all of the unknown keys in parallel. To determine a single key by brute force might take decades to complete, but as there are multiple targets the expected time to determine one of the key values becomes only a few days. Therefore there is a trade-off between the time spent on key generation and the time (and memory) spent on the brute force activity, which can be characterised as a "meet-in-the-middle" attack.
Bond also described a key binding problem. The CCA uses the common "two key" mode of 3DES, where keys consist of two halves, each a single DES key. The mode consists of encryption with the first half, decryption with the second and then encryption again with the first half. So-called "replicate keys" can be generated with both halves identical. In this case, two of the DES operations cancel out, making the key in effect a single DES key, and therefore suitable for inter-working with legacy systems. However, the CCA permits halves to be swapped at will between different keys. This binding problem means that if two replicate keys can be discovered, their halves can be swapped to create a full (non-replicate) 3DES key whose value is known.
Bond went on to combine these building blocks into several hypothetical attacks that were capable of compromising all the exportable keys in the device. However, the assembly of building blocks was only demonstrative, and his paper stopped short of actually describing attack code that could be deployed. Further investigation has made it clear that although the basic theory was correct, the security procedures in a banking environment would put extra requirements upon the attack that are not easy to fulfil.
To deploy any attack on a real-world bank, an attacker must circumvent a wide range of bank procedures that protect against fraud. These include:
Before we show how to defeat the dual control on the security module using Bond's techniques, it is instructive to consider why the attacker does not target the bank mainframe. If an attacker had control over this he could simply increase his bank balance, creating money from nowhere. But bank procedures are specifically designed to ensure that even with top-level access, covering up the evidence of such a change is very difficult, and sophisticated balancing checks would report an inconsistency.
To determine how the fraud was done, the internal auditors would consult the audit trails. Practically every action that takes place in a bank leaves a logging record behind, from international fund transfers right down to the times that staff enter and exit rooms. Given the size and complexity of these auditing systems, cleaning every record to remove details of unauthorised activity is a mammoth task. The need for redundancy in the face of failure means that many of the mainframe logs will be append-only files kept at multiple remote, physically secured, sites. There may be further trails to clean on other external machines and the attacker will only be able to guess whether the cover-up work is complete.
As an alternative to attacking the mainframe, security modules could be targeted. They do have much better physical security than other bank systems (for instance, the IBM 4758 is validated to FIPS 140-1 Level 4, which is the highest commercial evaluation level attainable). However, access to their software API is poorly audited, and the conditions under which to raise an alarm are badly understood. For instance, in order to steal PINs, the attacker need only breach the confidentiality of data rather than damage its integrity. The data flowing out of security modules is encrypted and the programmers creating the audit procedures may not fully understand the consequences of access to this "unreadable" data and fail to record all of the relevant events.
Bond's attack has the potential to defeat the dual controls on the CCA software within the 4758 and steal PIN derivation keys (or encryption keys for randomly chosen PINs), and this unauthorised activity would be likely to go unnoticed. But to manufacture false cards for use with stolen PINs, access to the mainframe database is needed to retrieve account information. If the attacker chooses the right access point, he could passively observe genuine database accesses, or could camouflage his requests by mixing them in with other traffic. It is definitely possible to collect this information stealthily, but there is always a risk that a particular sequence of events will be flagged as unusual and a detailed manual inspection triggered. The sooner the fraud is complete the better.
Similar time constraints apply to attacks on "Bills of Lading" systems, which are also protected by security modules. Here, the assets might be the multi-million pound cargo of an oil tanker that is in transit at sea for a month. If a corrupt insider can defeat the security module and sell the same oil twice, he will want the maximum possible time before the deception is detected.
Thus, in all attack scenarios the risk of early detection and the weight of evidence remaining must be assessed. The attacker needs to buy as much time as possible in which to launder money and assume a new identity.
Unfortunately, naïve application of Bond's "meet-in-the-middle" approach to key extraction from the CCA does not make for a promising attack. It requires multiple DES keys to be discovered, with each discovery providing data for the next stage of the attack. The source data has to be collected in three separate sessions of unauthorised access to the security module, with the cracking intervals between sessions lasting from a week to a month, depending upon the computing power available to the attacker. This exposes the attacker to considerable risk of detection and if one of the earlier sessions triggers an investigation it gives the authorities the opportunity to catch him "red-handed".
We therefore set out to optimise the key extraction attack with two main goals in mind:
Straightforward assembly of Bond's building blocks results in a three-stage attack:
(1) Test Pattern Generation: Discover a normal data encryption key to use as a test pattern for attacking an exporter key. This is necessary because exporter keys are only permitted to encrypt other keys, not chosen values. The method is to encrypt a test pattern of binary zeroes using a set of randomly generated data keys, and then to use the meet-in-the-middle attack to discover the value of one of these data keys.
(2) Exporter Key Harvesting: Use the known data key from stage (1) as a test pattern to generate a second set of test vectors for a meet-in-the-middle attack that reveals two double-length replicate exporter keys (replicate keys have both halves the same, thus acting like single DES keys). Once this stage is complete, the values of two of the keys in the set will be known.
(3) Valuable Data Export: Retrieve the valuable key material (e.g. PIN derivation keys). This requires a known double-length exporter key, as the CCA will not export a 3DES key encrypted under a single DES exporter key, for obvious security reasons. Here, the key-binding flaw in the CCA software is used to swap the halves of two known replicate keys from stage (2) in order to make a double-length key with unique halves. This full 3DES key can then be used for the export process.
In order to perform the attack in a single access session, the second set of test vectors had to be generated immediately after the first. However, it was not possible to know in advance which data key from the set would be discovered by the search, in order to use it as a test pattern. Generating a second set of test vectors for every possible data key would work in principle, but the number of operations the security module would have to perform would be exponentially increased, and at the maximum transaction rate (roughly 300 per second) would take ten days of unauthorised access.
So the first stage of the online attack had to yield the value of a particular data key that was chosen in advance, which could then be used as the test pattern for the second stage. The solution was to create a "related key set" using the Key_Part_Import command as described in Bond's paper. From the discovery of any single key, the values of all of the rest can be calculated. This related key set was made by generating an unknown data key part and XORing it with 214 different known values (the integers 0...16383 were used). Any one of the keys could then immediately be used for the second stage of the attack, even though its actual value would only be discovered later on.
The second stage was to export this single data key under a set of double-length replicate exporter keys and to use a meet-in-the-middle attack on the results. Two keys needed to be discovered so that their halves could be swapped to create a non-replicate exporter key. Once again the same problem arose in that it would be impossible to tell in advance which two keys would be discovered, and so the valuable key material could not be exported until after the cracking was complete. Generating a set of related exporter keys again solved the problem. Discovering just one replicate key now gave access to the entire set. Thus a double-length exporter with unique halves could be produced prior to the cracking activity by swapping the halves of any two of the related keys.
Implementation of this second stage of the process revealed an interesting and well-hidden flaw in the Key_Part_Import command. Although the concept of binding flaws had already been identified in the encrypted key tokens, it was also present in Key_Part_Import. It was possible to subvert the creation of a double-length replicate key so as to create a uniquely halved double-length key by the simple action of XORing in a new part with differing halves. This second instance of the flaw would have been missed had the theory not actually been implemented "for real". From the point of view of the system maintainer, this demonstrates the well-known principle that when generic weaknesses have been identified in an API, equally generic solutions should be sought, and patching individual parts of the transaction set is unlikely to solve all of the problems.
Finally, the new double-length exporter key made from the unknown replicate key part from stage two was used to export the valuable key material.
Although the attack still has three conceptual stages, there is no dependency on knowing the actual values of keys during the period of access to the 4758, so the stages can be run in a single session and the cracking effort done in retrospect.
Bond's paper proposed using a home PC for the DES key cracking, reflecting the resources available to a real-world attacker. However, experimentally cracking a single key showed that a typical 800 MHz machine would take about 20 days to crack one key out of a set of 216, this being the maximum number of encrypted results that it is realistic to consider producing during a "lunch-break-long" period of access to the CCA software. The cost of getting "no questions asked" access to multiple PCs in parallel is substantial, so a faster method was desirable in order to reduce the risk of the bank spotting the unauthorised access to the 4758 before the attack was complete.
DES was designed to work well with the integrated circuits of the mid-1970s and it has proved to be difficult to create high-speed software implementations on contemporary processor architectures. Hardware solutions are known to be many orders of magnitude faster than software crackers running on general purpose PCs. We therefore investigated the capabilities of modern FPGA systems. High-level hardware design languages such as Verilog allow them to be programmed by relative amateurs, so this was not stepping outside of the attack scenario. We became particularly interested in Altera's "Excalibur" NIOS evaluation board [1], which is an off-the-shelf, ready-to-run, no-soldering-required system that comes complete with all the tools necessary to develop systems such as a DES cracker. Altera's generosity meant that we got our board free; other attackers would be able to purchase it for US$995.
The basic idea of a brute force "DES cracker" is to try all possible keys in turn and stop when one is found that will correctly decrypt a given value into its plaintext. Sometimes, the plaintext that is to be matched is known, as in this case, and sometimes the correct decryption can only be determined statistically or through an absence of unacceptable values (for example, in the RSA decryption challenges posed in the late 1990s [16], the decrypted output needed to resemble English text).
This cracker design actually works the other way round; it takes an initial plaintext value and encrypts it under incrementing key values until the encrypted output matches one of the values being sought. The design runs at 33.33 MHz, testing one key per clock cycle, which is rather slow for cracking DES keys -- and it would take, with average luck, 34.6 years to crack a single key. However, the attack method allows many keys to be attacked in parallel and because they are interrelated it does not matter which one is discovered first.
The design was made capable of cracking up to 16384 keys in parallel (i.e. it simultaneously checks against the results of encrypting the plaintext with 16384 different DES keys). The particular Excalibur board being used imposed the 16384 limitation; if more memory had been available then the attack could have proceeded more quickly. The actual comparison was done in parallel by creating a simple hash of the encrypted values (by XORing together groups of 4 or 5 bits of the value) and then looking in that memory location to determine if an exact match had occurred. Clearly, there is a possibility that some of the encrypted values obtained from the 4758 would need to be stored in identical memory locations. We just discarded these clashes and collected rather more than 16384 values to ensure that the comparison memory would be reasonably full.
As already indicated, 69.2 years are necessary to try all possible keys and therefore guarantee a result. However, probabilistic estimates can be made of the likely running time. These estimates are valid because so many keys are being searched for, and because DES can be viewed as creating essentially random encrypted values (approximating a random function being a property of good crypto algorithms). Over a full search, the average time to find the next key can be calculated, by simple division, to be about 37 hours. However, it is more useful to consider the time to find the first key and model the system using a Poisson distribution. The probability that the first r attempts will all fail is e-λ r where λ is the probability any given attempt matches, which if checking against 16384 keys will be: 214 / 256 = 2-42. At 33.33 MHz with average luck (p = 0.5), the first key will be found within 25.4 hours. With bad luck (p = 0.001, i.e. all except one run in a thousand) the first key will be found within 10.5 days.
As already indicated, the attack requires two cracking runs, so one would hope to complete it in just over 2 days. In practice, the various keys we searched for were found in runs taking between 5 and 37 hours, which is well in accordance with prediction.
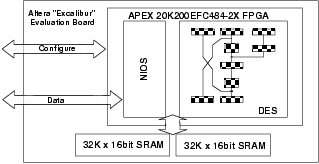
The DES cracker was implemented on the Altera Excalibur NIOS Development board [1]. This board contains an APEX EP20K200EFC484-2X FPGA chip which contains 8320 Lookup Tables (LUTs) -- equivalent to approximately 200,000 logic gates. The FPGA was programmed with a DES cracking design written in Verilog alongside of which, within the FPGA, was placed a 16-bit NIOS processor. The NIOS is an Altera developed RISC design which can be easily integrated with custom circuitry. The NIOS processor runs a simple program (written in GNU C and loaded into some local RAM on the FPGA) which looks after a serial link. The test vectors for the DES crack are loaded into the comparison memory via the serial link, and when cracking results are obtained they are returned over the same link. Although the NIOS could have been replaced by a purely hardware design, there was a considerable saving in complexity and development time by being able to use the pre-constructed building blocks of a processor, a UART and some interfacing PIOs. Fig. 1 shows the general arrangement:
 |
A pipelined version of the DES algorithm was used with the same input data value being encrypted by a succession of key values. At each clock interval, the intermediate left/right results of each DES stage are clocked into the next set of registers to act as inputs for the next stage of the encryption. Therefore, after an initial start-up period of 16 clocks, results appear from the end of pipeline at the clock rate of 33.33 MHz.
The key value must remain available for use by every stage of the algorithm, however we avoided the need to provide registers to pipeline its value from stage to stage. Instead, we used a Linear Feedback Shift Register (LFSR), which has been extended beyond its 56-bit value so that as it shifts, the extra bits serve to keep a record of older values of the key. This extended register is then statically connected, in an appropriate manner, to provide the key for the various pipeline stages. This space-saving technique was previously used by Hamer and Chow in their Transmogrifier DES cracker design [8]. The use of the LFSR had the further benefit of searching key space in a pseudo-random manner, so the 4758 programs were able to use densely packed sets of key values.
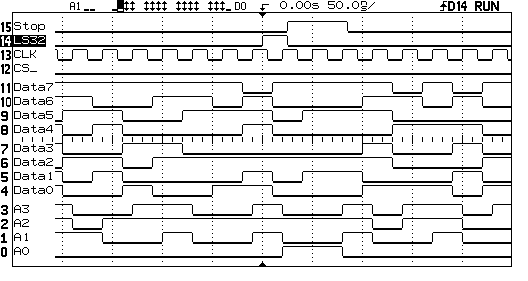
A tedious complication was that the Altera board has a limited amount of RAM as standard, just two 32K X 16-bit SRAMs. These could be arranged to form a single 32K X 32-bit memory, but it was still necessary for the 64-bit comparison to be done in two halves. If the first half matches (as will happen every few seconds) then the pipeline must be suspended for a moment and the second half of the value checked.
This can be seen on the logic analyser picture in Fig. 2 below. The regular signal on the third trace is the clock. The second signal down shows a 32-bit match is occurring. This causes a STOP of the pipeline (top signal) and access to an odd numbered address value (bottom signal). The other signals are some of the data and address lines.
 |
Although most of the cracker design was straightforward, the implementation of the DES S-boxes is of some interest. There are eight of these, each taking six bits of input and providing a 4-bit result. The S-boxes provide the non-linear component within the DES algorithm and they are defined in FIPS-46 [15] as tables of values that appear to be completely random.
The simplest way to implement the S-boxes would be as 128 read-only memories (8 for each of the 16 pipeline stages). Unfortunately, although the particular Altera FPGA architecture being used can be programmed to provide ROMs, only 52 were available on the particular chip being used. Therefore, the S-boxes had to be created from logic components. Hamer and Chow [8] (who used the same FPGA architecture) observed that one could create the 6-bit LUTs needed for the S-box bits from six 4-bit LUTs as shown in Fig. 3:
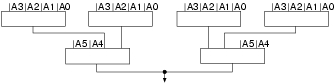 |
The final OR of the results is achieved "for free" by the FPGA circuitry. This gives a LUT count for each S-box of 24, giving an overall usage of 3072 LUTs for the whole design. This is over a third of the entire chip (8320 LUTs).
Because multi-level logic minimisation is complex, some optimal solutions may be missed. In order to ensure that the logic synthesis program would use the Hamer/Chow scheme, we wrote the Verilog for the S-boxes as follows:
wire [5:0] A = {address[5], address[0], address[4:1]};
reg [3:0] row0, row1, row2, row3;
always @(A)
begin
case (A[3:0])
0: begin row0 = 14; row1 = 0; row2 = 4; row3 = 15; end
... etc etc
15: begin row0 = 7; row1 = 8; row2 = 0; row3 = 13; end
endcase
case ({A[5],A[4]})
0: result = row0;
1: result = row1;
2: result = row2;
3: result = row3;
endcase
end
However, when making S-box 4, the logic minimisation process managed to save a couple of LUTs. This was of considerable interest because the design was clearly going to be quite a tight fit into the FPGA, so it was investigated further.
As can be seen by inspecting the code, the use of A0...A3 in the first stage and A4...A5 in the second stage is essentially arbitrary. The same result is obtained using another selection of 4 and then 2 bits by suitable alteration of the A[i] in the case statements. All of the 720 possible arrangements were tried, for each of the eight S-boxes. The result was that several other S-boxes were found to exhibit small amounts of non-randomness:
| S-box | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| LUTs | 24 | 23 | 23 | 16 | 24 | 24 | 23 | 22 |
Thus at each pipeline stage, 13 LUTs can be saved (almost 7% of the total).
This was not an entirely surprising result, although this is a new way of finding it. It has long been known that the DES S-boxes do have some internal structure [9,17,3] and in the 1970s this led some people to conclude that there were back doors into the DES system, especially since the NSA were said to have been involved in the S-box designs.
Key-cracking machines can be constructed at two extremes of system architecture. The cryptographic primitive can be arranged in a loop with a counter, as would be usual in a software implementation, or the loop can be "unrolled" to create a pipelined design. Between these two extremes, one can create hybrids where a few stages are pipelined and a lower maximum value of loop counter is used. No matter what the architecture, provided there is room within the FPGA, it is possible to add further instances of the basic design in parallel so as to provide a performance increase. It is interesting to consider which of these architectures is in fact optimal.
Experiments showed that a "loop" architecture duplicated 16 times, along with the logic to select results from each loop unit in turn, occupied 11,662 LUTs. In contrast, a fully pipelined architecture occupied 8,303 LUTs. Exactly the same performance might be expected from both designs; there is a start-up delay of 16 clocks and then they deliver one encrypted value on every subsequent clock. Therefore, it might seem that the pipeline design is to be preferred.
However, if one's FPGA is not large enough to hold the design (and it appears to be a fundamental rule of systems design that one inevitably runs out of gates or pins) then the pipelined architecture will not be implementable since it is "all or nothing". In contrast one can remove loop units to produce a cut-down design that delivers, for example, 10 results per 16 clocks. The saving is approximately 540 LUTs per loop unit (logic minimisation effects mean that the exact saving can vary). This might make the loop architecture preferable.
Historically, designs were always of the loop variety [5,4] because until relatively recently it was an achievement to get the whole of a single loop unit into a chip. By 1993, chips were larger and Wiener [18] proposed a pipelined design. However, although he used an LFSR to avoid the difficulty of a "ripple carry" across a 56-bit counter, he did not use the Hamer/Chow insight into how this could be used to avoid pipelining the key values. Kaps and Paar investigated several different FPGA designs [14], though their interest was in determining how pipelining or partial loop unrolling affected maximum clock speed. In the current work, the limiting speed was the external SRAM, so there was no benefit in making the cracker design run faster since all of the designs generated results faster than they could be compared against the set of encrypted values.
Speed and size are not the only constraints. The first machine to be actually constructed, the Electronic Freedom Foundation's (EFF) design [6], used a multiple loop unit design. A pipelined scheme was considered, but was rejected as being more complex and hence more risky for a project that needed to work first time [7].
One must conclude that there is no easy solution here. The optimal design approach seems to be to try the pipelined design first. If that does not fit into a particular chip then it will be necessary to discard the work done thus far and create a design that crams in as many loop units as possible.
Although many paper designs for DES cracking machines were proposed in the 1970s [5], 1980s [4] and 1990s [18], no publicly known machines were actually constructed until the Electronic Freedom Foundation built Deep Crack in 1998 [6]. This was an ASIC gate-array design, since this was the cheapest way of building it. Other work has been done before and since on FPGA based cracker designs such as [14,8] and most of these designs appear to have been synthesised and tested. However, the current work appears to be the first FPGA DES cracker design in the open literature (and only the second actual system after the EFF machine) that has actually found a key "in anger". Of course this achievement could only be done so quickly and for such a low cost because of the "meet-in-the-middle" nature of the problem we tackled.
The full attack described in this paper was run on two occasions in 2001 at the full rate of 33.33 MHz (approx. 225 keys/second). In both cases the expected running time of 50.8 hours (based on average luck in locating a key) was comfortably beaten and so it would have been possible to start using the PIN derivation keys well before unauthorised access to the 4758 would have been detected.
| Date | Start | Finish | Duration | Key value found |
| Aug 31 | 19:35 | 17:47 | 22 h 12 min | #3E0C7010C60C9EE8 |
| Sep 1 | 18:11 | 23:08 | 4 h 57 min | #5E6696F6B4F28A3A |
| Oct 9 | 17:01 | 11:13 | 19 h 12 min | #3EEA4C4CC78A460E |
| Oct 10 | 18:17 | 06:54 | 12 h 37 min | #B357466EDF7C1C0B |
We communicated our results to IBM. In early November 2001 they issued a warning to CCA users [11] cautioning them against enabling various functionality that the attacks depended upon. In February 2002 they issued a new version of the CCA software [12] with some substantial amendments that addressed all the issues raised by our attacks and those discussed by Bond in his earlier paper.
We have shown that the practical implementation of a theoretical attack is a worthwhile activity. Our research revealed aspects of both the system attacked and the attack method itself that would have been difficult to spot in any other way.
At the hardware design level we showed that pipelined implementations of DES could be made considerably smaller than designs using multiple looping units. We also found a new way of demonstrating that the DES S-boxes are not as random as they might at first appear.
At the conceptual level, we discovered a second specific instance of the generic key-binding flaw discussed in Bond's original paper. This highlights the risks of patching individual parts of a system to deal with security problems. Generic solutions must be sought for generic problems.
The specification-level faults that have been exploited in this attack have turned out to be just part of the story. Although we devoted some of our effort into reducing the effective strength of the CCA's 3DES implementation to that of single DES, IBM's analysis of our attack uncovered an implementation-level fault that made this whole stage unnecessary [13]. The CCA code was failing to prevent export of a double-length key under a double-length replicate key, despite the specifications stating that this would not be allowed.
In the future we must expect to see attacks that combine exploitation of both specification mistakes and faults in implementing the specification. It is hard to see how existing analysis practices at either the specification or the implementation level can hope to spot this type of hybrid. Making serious attempts to actually implement otherwise theoretical attacks may be our only handle on this problem.
We would like to acknowledge the generosity of Altera in providing the FPGA board used in this project for free. We'd also like to thank Ross Anderson and Simon Moore for their helpful comments and encouragement throughout. Mike Bond was able to conduct the research thanks to the funding received from the UK Engineering and Physical Research Council (EPSRC) and Marconi plc.