Foundations of Computer Science Supervision Work
Table of Contents
Please send in work by e-mail 48 hours before the supervision. Scanned copies are okay, you don't have to typeset the work, as long as it is legible. Please convert any Microsoft Word documents to PDF before sending.
Writing neat OCaml code
When programming, you are writing the code for two purposes: to execute, and to document what the code does. Here are some of my suggestions. They are more like guidelines than strict rules, if breaking these makes the code easier to read, do so. Also, if you are working on a large project, obey the project's coding style, rather than have multiple styles scattered in the project. (Programmers like neat regular patterns.)
- Line length
- Please try to limit the maximum line length to 80
characters. In Vim, you can use the
gq<motion>command to wrap long lines; in Emacs you can use M-q. There is:set colorcolumn=80in Vim, andfill-column-indicatorin Emacs. - Indentation
- A general advice is to avoid tabs, but this is not a
hard and fast rule, some people advocate using tabs
only for indentation, and spaces for everything
else. But whatever you do, do not mix tabs and
spaces in the same unit of whitespace. See Vim's
ts,stsandetoptions, or Emacs'tab-widthandindent-tabs-modesettings. - Alignment
- Try to make your code read nicely
- Naming
Try to make the functions and value names be descriptive (you don't have to do a Java and write poems with names though, the following was a single Java class name [without spaces or line-breaks]:
InternalFrame
InternalFrame
TitlePane
InternalFrame
TitlePane
MaximizeButton
WindowNotFocusedState
though I believe that name was auto-generated). If you cannot find a single (common) word for what the function/value stands for, you should comment.
- Comments
- Comments should not state what is obvious from reading the code, they are there for things like functions that don't have an obvious name, obscure behaviour you rely on, and other things that I cannot think of at the moment.
- Parentheses
Don't over-parenthesise, but also don't rely on people knowing all the operator precedences (it's a balance). E.g. you can rely on multiplication/division being more tightly binding than addition/subtraction, but relying on cons/append being less tightly binding than addition isn't necessarily obvious. If you do use that, you might want to make a comment.
If you have parentheses spanning multiple lines, make the indentation act as a hint to the parenthesisation.
- Pattern Matching
- If it makes sense, try to match all the
cases. If it doesn't, raise a useful error; figuring out where
that
Matchexception came from is not pleasant. - Conditionals
If they are too deeply nested, perhaps the code needs refactoring. If one or both branches of a conditional return either
trueorfalse, try usingnot,||and&&.a (* instead of *) if a then true else false not a (* instead of *) if a then false else true a || b (* instead of *) if a then true else b a && b (* instead of *) if a then b else false
- Let expressions
- They help give your code useful names, and break up big expressions into manageable chunks.
Making OCaml coding more pleasant
OCaml doesn't have a go-to IDE, but do use a programmer's editor (in
alphabetical order: Atom, Emacs, SublimeText, Vim, …). Notepad (not
Notepad++) isn't a programmer's editor, nor is Microsoft Word (you
can use them, but they don't help you, unlike a programmer's
editor). Install merlin for your editor if you want tab completion.
Use the #use <filename>;; directive. It loads from the directory
where you started the interpreter, in Mac/Linux, this is the terminal
window into that you had open when you typed ocaml or utop. In
Windows, you can right-click the shortcut and customize the
directory. You can change directories with #cd <path>;;. Install
utop to have a better time with the REPL (e.g. history, arrow-keys,
completion).
To get the hang of debugging type errors, make a couple of deliberate ones, and read the error it throws at you, already knowing what the error is.
Further info at https://ocaml.org/learn/tutorials/get_up_and_running.html
1 Work for Supervision 1
1.1 Exercise 1 [floating point]
Another example of the inaccuracy of floating-point arithmetic takes the golden ratio \(φ ≈ 1.618\ldots\) as its starting point:
\[γ_0 = \frac{1 + \sqrt{5}}{2} \quad\text{and}\quad γ_{n + 1} = \frac{1}{γ_n − 1}.\]
In theory, it is easy to prove that \(γ_n = \cdots = γ_1 = γ_0\) for all
\(n > 0\). Code this computation in OCaml and report the value of
\(γ_{50}\). [Hint: in OCaml, \(\sqrt{5}\) is expressed as
sqrt 5.0.] [2 marks]
1.2 Exercise 2 [recurrence equations]
Find an upper bound for the recurrence given by \(T (1) = 1\) and \(T (n) = 2 T (n / 2) + 1\). You should be able to find a tighter bound than \(O (n \log n)\). [4 marks]
1.3 Exercise 3 [tail recursion]
Code a tail-recursive version of: [4 marks]
let even n = (n mod 2) = 0 let rec power(x, n) = if n=0 then 1 else if even n then power(x*x, n/2) else x * power(x*x, (n-1)/2)
1.4 Two of
1.4.1 Option 1
- “We face the Year 2000 crisis because programmers did not apply the principles of data abstraction.” Discuss. [4 marks]
Your employer asks you to implement a dictionary. The pattern of usage will consist of taking an empty dictionary and performing many insertions and lookups. You must choose one of three data structures. Each requires \(O(\log n)\) time for the lookup and update operations, where n is the number of items in the dictionary. They are (1) binary search trees, which take \(O(\log n)\) time in the average case; (2) balanced trees, which need complicated algorithms but take \(O(\log n)\) time in the worst case; (3) self-adjusting trees, which take \(O(\log n)\) amortised time in the worst case.
Explain the differences between the three notions of \(O(\log n)\) time. Argue that any of the three data structures might turn out to be the best, depending upon further details of the application. If no further details are available, which of the three is the safest choice? [8 marks]
An algorithm requires \(T(n)\) units of space given an input of size \(n\), where the function \(T\) satisfies the recurrence
\begin{align*} T(1) &= 1 \\ T(n) &= T(n/2) + n \quad\text{for } n > 1. \end{align*}Express the algorithm’s space requirement using O-notation, carefully justifying your answer. [8 marks]
1.4.2 Option 2
- Explain how \(O\text{-notation}\) is used to express efficiency of algorithms. [5 marks]
Arrange the following list of complexity classes in order of decreasing efficiency in n. Briefly justify each relationship. [4 marks]
\[ O(5n^2) \quad O(e^n) \quad O(n^{1/3}) \quad O(n^3 − 3n^2) \quad O(\log n) \quad O(n2^n) \]
- Suppose that \(f\) is a function from integers to integers
such that \(i\leq j\) implies \(f(i) \leq f(j)\). Then there
is an efficient algorithm to solve the equation \(f(k) =
y\), given the desired \(y\) and a range of values in which
to search for \(k\): the idea is repeatedly to halve this
range. Code this algorithm as the OCaml function
searchwhose arguments are \(f, y\), and the range \((a, b)\). Its result should be the greatest \(k\) such that \(f(k) \leq y\) and \(a \leq k \leq b\), provided such a \(k\) exists. [11 marks]
1.4.3 Option 3
Consider the following OCaml declarations:
type bit = One | Zero type cardinal = bit list exception Result_would_be_negative
Define functions to add, subtract and multiply
cardinals, viewing them as representations of
integers stored as in binary with the least significant bit
of the value first in the list. Thus for instance the number
eleven has the value 1011 in binary and so would be
represented (note the ordering of the bits) by the structure
Cardinal [one, one, zero, one] Using Big-O notation
state the time complexity of your add and multiply
functions. [20 marks]
1.4.4 Option 4
Give an example of a realistic OCaml function belonging to each of the following complexity classes:
- \(O(1)\); [2 marks]
- \(O(n)\); [2 marks]
- \(O(n \log n)\); [2 marks]
- \(O(n^2)\); [2 marks]
- \(O(2n)\). [2 marks]
Each answer may contain code fragments (involving well-known functions) rather than self-contained programs, but must include justification. Don't just code the recurrence equation as an OCaml function, the examples should do something useful, if possible. The upper bound in each case should be reasonably tight.
Estimate the time complexities of the functions
f1,f2, andf3: [10 marks]let rec f1 = function 1 -> 1 | n -> 1 + f1(n-1) let rec f2 = function 1 -> 1 | n -> f2(n-1) + f1 n let rec f3 = function 1 -> 1 | n -> f3(n/7) + f3(5*n/7) + f1 n;
2 Work for Supervision 2
2.1 Exercise 1
Give the data-type for lists, and the definition for functions map,
fold_left, fold_right.
type 'a list = ?? let rec map f list = ?? (* map f [x1; x2; ...; xn] = [f x1; f x2; ...; f xn] *) let rec fold_left f init list = ?? (* fold_left f init [x1; x2; ...; xn] = f ( ... (f (f init x1) x2) ... ) xn *) let rec fold_right f init list = ?? (* fold_right f [x1; x2; ...; xn] init = f x1 (f x2 ( ... (f xn init) ... )) *)
2.2 Exercise 2
The binary search tree t1 is superseded by t2 provided every entry
in t1 is also present in t2. Code an OCaml function to determine
whether one binary search tree is superseded by another. Express its
cost in terms of \(n_1\) and \(n_2\), the numbers of entries in t1 and
t2, respectively. For full credit, the worst-case cost should be no
worse than \(O(n_1 + n_2)\). [10 marks]
2.3 One of:
2.3.1 Option 1
The OCaml data type bool_exp, defined below, is to be
used to represent boolean expressions.
type bool_exp = Var of string | Not of bool_exp | And of bool_exp*bool_exp | Or of bool_exp*bool_exp
- The constructor
Varis used to represent named boolean variables, andNot,AndandOrare used to represent the corresponding boolean operators. Define a function that will return a list of the distinct names used in a given boolean expression. [4 marks] - A context is represented by a list of strings corresponding to the boolean variables that are set to true. All other variables are deemed to be set to false. Define a function that will evaluate a given boolean expression in a given context. [3 marks]
- Incorporate your two functions into a program that will determine whether a given boolean expression is true for all possible settings of its variables. [3 marks]
2.3.2 Option 2 (slightly more difficult)
- Run-length encoding is a way of compressing a list in
which certain elements are repeated many times in a
row. For example, a list of the form
[a; a; a; b; a; a]is encoded as[3, a; 1, b; 2, a]. Write a polymorphic functionrl_encodeto perform this encoding. What is the type ofrl_encode? [6 marks] The simple task of testing whether two lists are equal can be generalised to allow a certain number of errors. We consider three forms of error:
- element mismatch, as in
[1;2;3]versus[1;9;3]or[1;2;3]versus[0;2;3] - left deletion, as in
[1;3]versus[1;2;3]or[1;2]versus[1;2;3] - right deletion, as in
[1;2;3]versus[1;3]or[1;2;3]versus[1;2]
Write a function
genEquals n xs ysthat returns true if the two listsxsandysare equal with no more thannerrors, and otherwise returns false. You may assume thatnis a non-negative integer. [8 marks]- element mismatch, as in
2.4 One of:
2.4.1 Option 1
A permutation of a list is any list that can be derived from
it by re-arranging the elements. Write an OCaml function that
returns the list of all the permutations of its
argument. Explain your code clearly and carefully. For
example, applied to the list [1;2;3], your function
should return the list whose elements are [1;2;3],
[2;1;3], [2;3;1], [1;3;2],
[3;1;2] and [3;2;1]. You may assume that
the elements of the argument are distinct. The elements of
the result may appear in any order. [10 marks]
2.4.2 Option 2 (more difficult)
- A binary tree is either a leaf (containing no information) or is a branch containing a label and two subtrees (called the left and right subtrees). Write OCaml code for a function that takes a label and two lists of trees, returning all trees that consist of a branch with the given label, with the left subtree taken from the first list of trees and the right subtree taken from the second list of trees. [6 marks]
Write OCaml code for a function that, given a list of distinct values, returns a list of all possible binary trees whose labels, enumerated in inorder, match that list. For example, given the list
[1;2;3]your function should return (in any order) the following list of trees: [8 marks]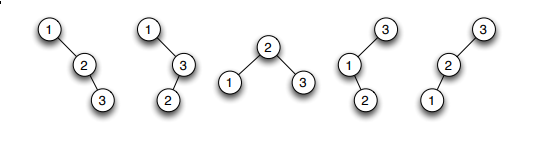
2.5 One of:
2.5.1 Option 1
- Write brief notes on exceptions in OCaml and on the functions and control structures available for programming with them. [6 marks]
The following parts require the following exception
exception Redo_from_start;
- Code in Ocaml a function called
cannotwhich takes two arguments (curried), a functionfand a valuex. Define thecannotfunction in such a way that it returns true if and only if evaluation off(x)causes the exceptionRedo_from_start. For all other inputs, it should return false. [Hint: evaluation off(x)may cause exceptions other thanRedo_from_start.] [4 marks] Consider the following OCaml datatype and functions
hexandstibbons.type 'a tree = Leaf of 'a | Branch of 'a tree * 'a tree let rec hex (x, t) = match t with | Leaf y -> if x=y then raise Redo_from_start else Leaf y | Branch (t1, t2) -> Branch (hex (x, t1), hex (x, t2)) let stibbons x t = if cannot hex (x, t) then Leaf x else hex(x, t)
- Write down the type of
stibbons. [3 marks] - Write a function that is equivalent to
stibbonsbut makes no use of exceptions. Briefly explain why your function is equivalent tostibbons. [7 marks]
- Write down the type of
- Code in Ocaml a function called
2.5.2 Option 2
Consider the following piece of OCaml code:
type 'a tree = Lf | Br of 'a * 'a tree * 'a tree exception Out_of_cheese let rec anthill p t = match t with | Lf -> true | Br (x, t1, t2) -> if not (p x) then raise Out_of_cheese else try anthill p t1 with Out_of_cheese -> anthill p t2 let hex p t = try anthill p t with Out_of_cheese -> false
- Code a function that returns the same results as
hexbut makes no use of exceptions. [4 marks] - What property of binary trees does
hexexpress? [3 marks]
- Code a function that returns the same results as
- Write brief notes on the OCaml type
exn. [3 marks] Consider the following piece of OCaml code:
type 'a result = Ridcully of 'a | Rincewind of exn let what f x = try Ridcully (f x) with e -> Rincewind e
We ask OCaml to evaluate the expression
map (what (anthill (fun x -> x <> 0))) [ta;tb]and the response is as follows:val it : bool result list = [Ridcully true; Rincewind Out_of_cheese]What is the type ofwhat (anthill (fun x -> x <> 0)), and what can we infer about the binary treestaandtb? Justify both answers carefully.
[5+5 marks]
3 Work for Supervision 3
3.1 One of [first class functions]:
3.1.1 Option 1
This question uses the following datatype
type 'a fan = Wave of 'a * ('a fan list);
- Declare the function
flip, which maps a tree to a mirror image of itself, as illustrated: [3 marks]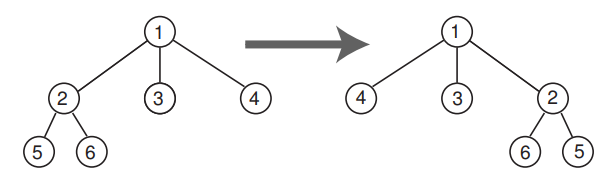
- Declare the curried function
paint f, which copies a tree while applying the functionfto each of its labels. [3 marks] - Declare the function
same_shape, which compares two trees and returns true if they are equal except for the values of their labels and otherwise returns false. [5 marks] - State the types of functions
flip,paintandsame_shape. [3 marks] The function paper is declared in terms of the familiar functional
foldr:let rec fold_right f tree_list init = match tree_list with | [] -> init | x::xs -> f x (fold_right f xs init) let rec paper fan q = match fan with Wave(el, fans) -> fold_right paper fans (q+1)
Describe the computation that results when
paperis applied to a tree. Can you sketch an inductive proof? [6 marks]
3.1.2 Option 2
- Write brief notes on polymorphism in OCaml, using lists and
standard list functions such as
@(append) andList.map. [4 marks] Explain the meaning of the following declaration and describe the corresponding data structure, including the role of polymorphism.
type 'a se = Void | Unit of 'a | Join of 'a se * 'a se;
[4 marks]
- Show that OCaml lists can be represented using this datatype by
writing the functions
encode_listof type'a list -> 'a seanddecode_listof type'a se -> 'a list, such thatdecode_list (encode_list xs) = xsfor every listxs. [3 marks] Consider the following function declaration:
let rec cute p = function | Void -> false | Unit x -> p x | Join (u,v) -> cute p u || cute p v;
What does this function do, and what is its type? [4 marks]
Consider the following expression:
fun p -> cute (cute p)
What does it mean, and what is its type? Justify your answer carefully. [5 marks]
3.2 One of [functional arrays]:
3.2.1 Option 1
- Write brief notes about a tree representation of functional arrays, subscripted by positive integers according to their representation in binary notation. How efficient are the lookup and update operations? [6 marks]
- Write an OCaml function
arrayoflistto convert the list \([x_1; \ldots ; x_n]\) to the corresponding functional array having \(x_i\) at subscript position \(i\) for \(i = 1,\ldots, n\). Your function should not call the update operation. [6 marks] - Consider the task of finding out which elements of an
array satisfy the predicate
p, returning the corresponding subscript positions as a list. For example, the list \([2; 3; 6]\) indicates that these three designated array elements, and no others, satisfyp. Write an OCaml functional to do this for a given array and predicate, returning the subscripts in increasing order. [8 marks]
3.2.2 Option 2
- In OCaml it is possible to use functions as values: they can be passed as arguments and returned as results. Explain the notation used to write a function without having to give it a name. [2 marks]
One possible functional implementation of an array is based on trees, and the path to a stored value follows the binary code for the subscript:
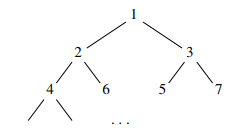
where in the above diagram the numbers show where in the tree a value with the given subscript will live. Write code that creates, retrieves values from and updates an array that has this representation, and using big-O notation explain the associated costs. [8 marks]
A different way of handling functional arrays is to represent the whole array directly by a function that maps from integers to values. To access the item at position k in such an array you just use the array as a function and give it k as its argument, and to update the array you need to create a new function reflecting the changed value.
If the array is to hold integer values, what OCaml type does it have? [1 mark]
Write a function
update a n vwhere a is a functional array in this style,nis an integer index andvis a new value. The result of the call to update must behave as an array that stores all the values that a did except that it is as if an assignment of the stylea[n] := vhas been performed. [5 marks]In big-O notation, what is the cost of your
updatefunction? After a sequence of updates what is the cost of accessing the array? [4 marks]
3.3 Exercise 3 [lazy lists]
The datatype 'a lazy_list defined below is to be
used for the representation of priority queues which are
finite or infinite ordered sets of integers.
type 'a lazy_list = Nil | LCons of 'a * (unit -> 'a lazy_list)
- Define an OCaml function
intfromto(i,j) : (int*int)->int lazy_listwhich will return a representation of the ordered set of integers \([i; i+1; \cdots, j]\). Define the function
first(p) : 'a lazy_list -> 'athat will return the first (and hence smallest) integer in the given queuep, andrest(p) : 'a lazy_list -> 'a lazy_listthat will return (if possible) a representation of the given queuepwith its smallest element removed.Your implementation should be such that the expression
first(rest (intsfromto(20, 1000000)))should evaluate efficiently.- Define an OCaml function
ins i p : int -> int lazy_list -> int lazy_listwhich will return a priority queue with the integeriinserted in the proper position of the given queuep(insert even if aniis already present). [10 marks]
3.4 One of [laziness]:
3.4.1 Option 1
- Define an OCaml datatype for infinite lists, without the
possibility of finite lists. Briefly illustrate
programming techniques for your datatype by declaring
- a recursive functional (analogous to map for ordinary lists) that applies a given function to every element of an infinite list.
- a function for generating infinite lists of the form \(x, f(x), f(f(x)), \ldots\) for any given \(f\) and \(x\). [6 marks]
- Briefly explain why the function analogous to append (@) for ordinary lists is of no value for your infinite list data type. Code a function to combine two arbitrary infinite lists, yielding a result that includes the elements of both lists. [3 marks]
- Use the functions declared in your previous solutions to express an infinite list consisting of all numbers of the form \(5^i × 7^j × 9^k\) for integers \(i, j, k ≥ 0\). [3 marks]
- The list \([1; 5; 7; 25; 9; 35; 35; \ldots]\) is a legitimate solution to the previous part above, but note that the integers are out of order. Code a function to merge two ordered infinite lists, and use that to modify your previous solution to yield the same set of numbers but in strictly increasing order. Briefly comment, with justification, on whether merge-sort for ordinary lists can be generalised to infinite lists. [8 marks]
3.4.2 Option 2
- Describe how lazy lists, which have possibly infinite length, can be implemented in OCaml. Illustrate your answer by presenting a function that accepts one (or more) lazy lists and produces another lazy list. [6 marks]
- A lazy binary tree either is empty or is a branch containing a label and two lazy binary trees, possibly to infinite depth. Present an OCaml datatype to represent lazy binary trees. [2 marks]
- Present an OCaml function that produces a lazy binary tree whose labels include all the integers, including the negative integers. [3 marks]
- Present an OCaml function that accepts a lazy binary tree and produces a lazy list that contains all of the tree’s labels. [9 marks]
3.4.3 Option 3
The function perms returns all \(n!\) permutations of
a given n-element list.
let map, rev = List.(map, rev) let cons x y = x::y let rec perms = function | [] -> [[]] | xs -> let rec perms_inner ys = function | [] -> [] | x::xs -> map (cons x) (perms (rev ys @ xs)) @ perms_inner (x::ys) xs in perms_inner [] xs
- Explain the ideas behind this code, including the function
perms_innerand the expressionmap (cons x). What value is returned byperms [1;2;3]? [7 marks] A student modifies perms to use an OCaml type of lazy lists, where appendq and mapq are lazy list analogues of @ and map.
let cons x xs = x::xs let rec lperms = function | [] -> LCons([], fun () -> Nil) | xs -> let rec perms_inner ys = function | [] -> Nil | x::xs -> appendq (mapq (cons x) (lperms (rev ys @ xs))) (perms_inner (x::ys) xs) in perms_inner [] xs
Unfortunately,
lpermscomputes all \(n!\) permutations as soon as it is called. Describe how lazy lists are implemented in OCaml and explain why laziness is not achieved here. [5 marks]- Modify the function
lperms, without changing its type, so that it computes permutations upon demand rather than all at once. [8 marks]
3.4.4 Option 4
Consider a datatype of binary trees where both leaves and branches carry labels:
type 'a tree = Lf | Br of 'a * 'a tree * 'a tree;
A path in a binary tree is a series of labels proceeding from the root to a leaf, as shown in the diagram:
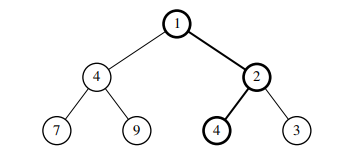
Consider the problem of finding a path in a binary tree such that every node of the tree satisfies a predicate, for example in the diagram above, the labels of the nodes are all powers of two.
- Write an OCaml function
find_path p twhich returns some path intwhere each value of the branch satisfies the boolean-valued functionp. If no such path exists, the function should raise an exception. [5 marks] - Write an OCaml function all paths such that
all_paths p treturns the list of all paths intwhose branches satisfy the boolean-valued functionp. [6 marks] - Write an OCaml function
all_pathqthat is analogous toall_pathsbut returns a lazy list of paths. For full credit, branches function should find paths upon demand rather than all at once. [9 marks]
4 Work for Supervision 4
4.1 Exercise 1 [imperative]
- Describe how OCaml lists are represented in storage. Your
answer should include diagrams illustrating how the
representation of
[a; b]@[c; d]is derived from those of the lists[a; b]and[c; d], indicating any sharing of memory. How efficient is the evaluation of[a; b]@lif the listlis very long? [4 marks] - Describe OCaml’s reference types and their applications. In particular, compare mutable data structures with ordinary OCaml datatypes. [2 marks]
- What are cyclic lists and how can they be created in OCaml
(creating the cycle manually, without using e.g.
let rec x = 1::x)? [6 marks] - Code an OCaml function that takes a mutable list and returns true
if the list is cyclic, otherwise returning false. Explain why your
function is correct. [Hint: in OCaml, the equality test
p == qis permitted on references and is true if p and q refer to the same location in memory.] [8 marks]
4.2 Exercise 2 [polynomial arithmetic]
To represent the power series \(\sum^∞_{i=0} a_i x^i\) in a
computer amounts to representing the coefficients \(a_0, a_1,
a_2, \cdots\). One possible representation is by a function
of type int->float that returns the coefficient
\(a_i\) given i as an argument. An alternative
representation is the following datatype:
type power = Cons of float * (unit -> power);
You may assume there is an OCaml function float of type int->float
that maps an integer to the equivalent floating-point number.
- Demonstrate the two representations by using each of them
to implement these two power series:
- The constant power series \(c\), with \(a_0 = c\) and \(a_i = 0\) for \(i > 0\). [3 marks]
- The Taylor series \(\sum^∞_{i=0} x^i/i!\) for the exponential function. [4 marks]
- Also implement (using both representations) each of the
following operations on power series:
- Product with a scalar, given by \(c \cdot \left( \sum^∞_{i=0} a_i x^i \right) = \sum^∞_{i=0} (ca_i) x^i\). [3 marks]
- Sum, given by \(\left( \sum^∞_{i=0} a_i x^i \right) + \left( \sum^∞_{i=0} b_i x^i \right) = \sum^∞_{i=0} (a_i + b_i) x^i\). [4 marks]
- The product \(\left(\sum^∞_{i=0} a_i x^i \right) × \left(\sum^∞_{i=0} b_i x^i \right)\), where the ith coefficient of the result is \(a_0 b_i + a_1 b_{i−1} + \cdots + a_i b_0\). [6 marks]
4.3 One of [search]:
4.3.1 Option 1
This question considers 2-dimensional rectangular labyrinths such as the following.
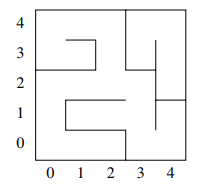
Here horizontal and vertical bars indicate walls. One can
step from a position to an adjacent position if there is no
wall obstructing the move. For example, one can move in one
step from position (1,1) to position (2,1), but not to
(1,0). Diagonal steps are not allowed.
- Carefully explain a convenient way of representing such
labyrinths in OCaml. Then define a function, call it next,
which takes two arguments, a position
(x,y)and a labyrinth, and returns a list of all positions that can be reached in one step from position(x,y). [Hint: Consider representing labyrinths as functions with a type of the formint * int -> something.] [8 marks] - Use next to code, in OCaml, a space-efficient function that
checks whether it is possible to move from a position
(x1,y1)to another position(x2,y2)in a given labyrinth. For full marks, make sure your function always terminates. [6 marks] - Explain, not necessarily using OCaml code, how one can code a function that returns the shortest path between two given positions. Here path means a list of all the positions one would visit en route to the destination. The solution must be space efficient and practical even for large labyrinths. Briefly explain why your solution is space efficient. [6 marks]
4.3.2 Option 2
A puzzle, or one-person game, can be represented in OCaml by two functions:
- a next-state function, which maps a state to a list of possible next states, and
- a wins function, which returns true if the given state counts as a win.
A simple example is a puzzle that has states consisting of
positive integers, a nextstate function that maps n to
[n+ 2, n+ 5], and a wins function that returns true if
n = 10. We can win if we start from n = 2 but not from
n = 7.
- Code a polymorphic datatype
'a puzzle, to represent a puzzle by the pair of a next-state function and a wins function. [2 marks] - Briefly contrast depth-first search, breadth-first search and iterative deepening as techniques for solving such puzzles. [6 marks]
- Write a function depth that accepts a puzzle, a state and a depth limit. It should use depth-first search to determine whether the puzzle can be solved from the given state within the given depth limit. [6 marks]
- Write a function breadth that accepts a puzzle and a state. It should use breadth-first search to determine whether the puzzle can be solved from the given state. [6 marks]