D&D Probability distributions

1. Dice averages
2. Advantage and Disadvantage
3. Multiple rolls

1 Dice averages

D4	D6	D8	D10	D12	D20
2.5	3.5	4.5	5.5	6.5	10.5

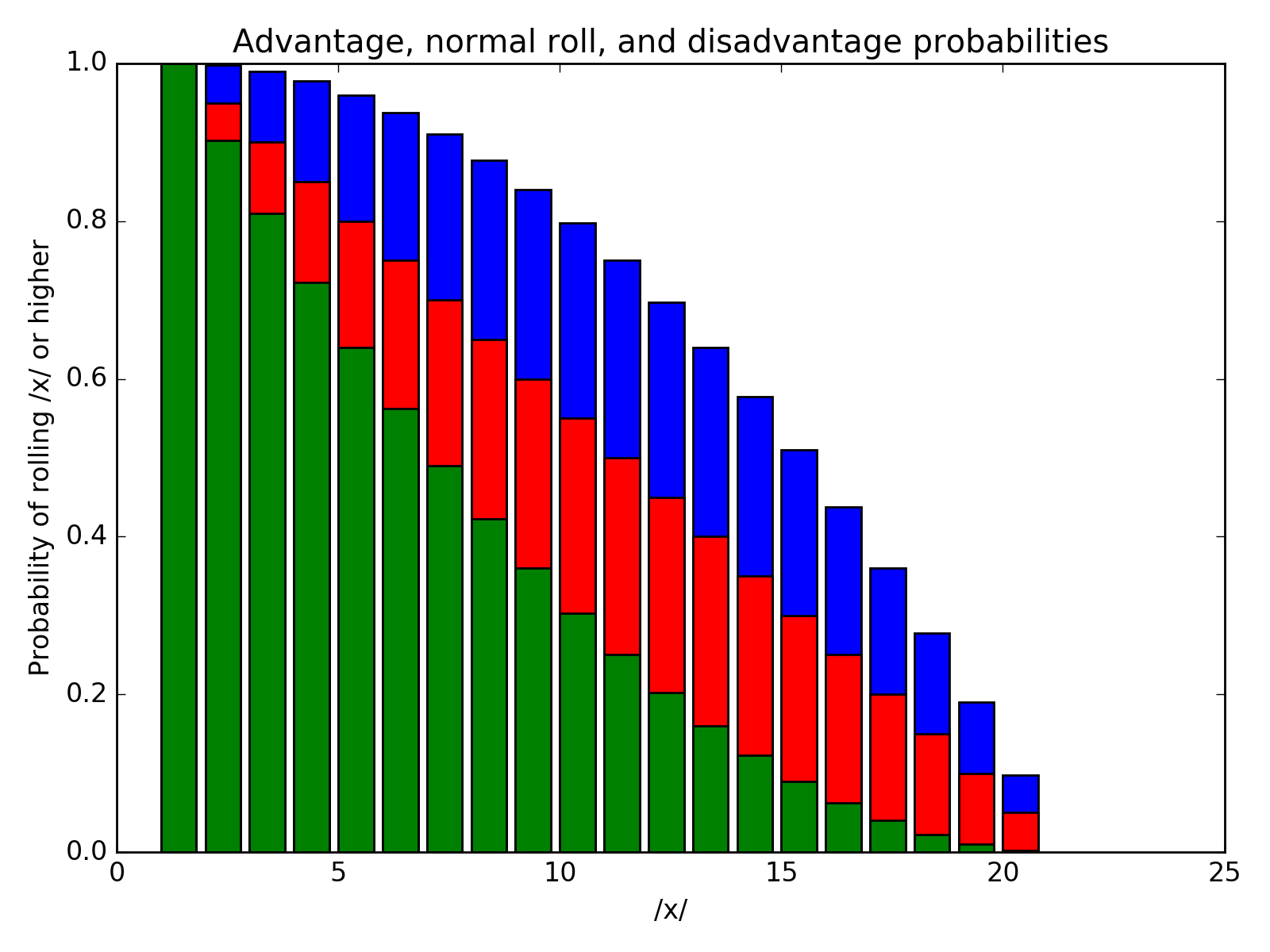
2 Advantage and Disadvantage

A normal, unweighted die has equal probabilities, so the cumulative probability distribution is just a straight line. However, the advantaged throws are much better, having

import numpy as np

d20 = np.arange(1,21)

disadvantage = (400-d20**2)/400.0
normal_roll = (20-d20)/20.0
advantage = ((20-d20)**2)/400.0
return np.array([d20.tolist(),
                 disadvantage.tolist(),
                 normal_roll.tolist(),
                 advantage.tolist()]) \
                 .transpose()

1.0	0.9975	0.95	0.9025
2.0	0.99	0.9	0.81
3.0	0.9775	0.85	0.7225
4.0	0.96	0.8	0.64
5.0	0.9375	0.75	0.5625
6.0	0.91	0.7	0.49
7.0	0.8775	0.65	0.4225
8.0	0.84	0.6	0.36
9.0	0.7975	0.55	0.3025
10.0	0.75	0.5	0.25
11.0	0.6975	0.45	0.2025
12.0	0.64	0.4	0.16
13.0	0.5775	0.35	0.1225
14.0	0.51	0.3	0.09
15.0	0.4375	0.25	0.0625
16.0	0.36	0.2	0.04
17.0	0.2775	0.15	0.0225
18.0	0.19	0.1	0.01
19.0	0.0975	0.05	0.0025
20.0	0.0	0.0	0.0

import numpy as np
import matplotlib.pyplot as plot

rollsNP = np.array(rolls)

fig, ax = plot.subplots()

d20 = np.arange(1,21)

ax.set_title("Advantage, normal roll, and disadvantage probabilities")
ax.set_xlabel("/x/")
ax.set_ylabel("Probability of rolling /x/ or higher")

plot.bar(rollsNP.T[0], rollsNP.T[1], color='blue', label="disadvantage")
plot.bar(rollsNP.T[0], rollsNP.T[2], color='red', label="normal roll")
plot.bar(rollsNP.T[0], rollsNP.T[3], color='green', label="advantage")

fig.tight_layout()
name = 'adv-disadv-plot.png'
fig.savefig(name, dpi=200)
return name

3 Multiple rolls

Binomial distribution

pmf	\({n \choose k}\,p^{k}(1-p)^{n-k}\)
CDF	\(\sum^{\lfloor k \rfloor}_{i=0} {n \choose i} p^i {(1-p)}^{n-i}\)
Mean	\(np\)
Median	\(\lfloor np\rfloor \text{ or } \lceil np\rceil\)
Mode	\(\lfloor (n+1)p\rfloor \text { or } \lceil (n+1)p\rceil -1\)
Variance	\(np(1-p)\)

were \({n\choose k} = \frac{n!}{k!(n-k)!}\) is the binomial coefficient (nCk on calculators), also known as choosing \(k\) subsets out of \(n\) elements.

D&D Probability distributions

Table of Contents

1 Dice averages

2 Advantage and Disadvantage

3 Multiple rolls