
John Daugman, University of Cambridge
It is useful to examine the relationship between False Accept probabilities when
attempting a
verification (a one-to-one comparison against a single stored
template), versus an identification (a one-to-many
comparison against all the enrolled biometric
templates in some database of size N). In this analysis,
we assume that the presenting template is not one of those enrolled, and so we
only consider False Accept probabilities. (Extension to the case of an enrolled
template is straightforward.)
Let P1 = probability of a False Accept in verification trials.
Let PN = probability of a False Accept in identification trials
after exhaustive search through a database of size N. We wish to compute
this.
Clearly the probability of not getting a False Accept on any given
trial is (1-P1). This must happen N independent times, and so the
probability of it not occuring on any of those N trials is
(1-P1)N.
Thus the probability of making at least one False Accept among
those N trials is just one minus that probability:
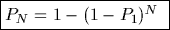
Example: Consider a biometric verifier that achieves a
99.9% Correct Rejection performance in verifications. Thus
P1 = 0.001 (one False Accept in 1,000 trials).
How will it perform when searching through a database?
Using the above expression, we see that for the following database sizes N,
these will be the probabilities PN that this verifier makes
at least one False Accept:
- Database of 200:
PN = 0.181 (False Accept probability 18%)
- Database of 2,000:
PN = 0.86 (False Accept probability 86%)
- Database of 10,000:
PN = 0.99995 (False Accept probability 99.995%)
Note that once the enrolled database size reaches about 7,000 persons, this
verifier becomes more likely (99.91%) to produce a False Accept in
identification trials than it
is to produce a Correct Rejection (99.9%) in verification trials!
Conclusion: Identification is vastly more demanding than
verification, and even for moderate database sizes, merely ``good" verifiers
are of no use as identifiers. Observing the approximation that
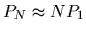 for small
for small
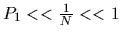 ,
when searching a database of size N an identifier needs to be
roughly N times better than a verifier to achieve comparable odds against a
False Accept.
,
when searching a database of size N an identifier needs to be
roughly N times better than a verifier to achieve comparable odds against a
False Accept.