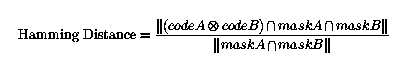
The key to iris recognition is the failure of a test of statistical independence, which involves so many degrees-of-freedom that this test is virtually guaranteed to be passed whenever the IrisCodes for two different eyes are compared, but to be uniquely failed when any eye's IrisCode is compared with another version of itself.
The test of statistical independence is implemented by the simple Boolean Exclusive-OR operator (XOR) applied to the 2,048 bit phase vectors that encode any two iris patterns, masked (AND'ed) by both of their corresponding mask bit vectors to prevent non-iris artifacts from influencing iris comparisons. The XOR operator detects disagreement between any corresponding pair of bits, while the AND operator ensures that the compared bits are both deemed to have been uncorrupted by eyelashes, eyelids, specular reflections, or other noise. The norms (|| ||) of the resultant XOR'ed phase bit vectors and of the AND'ed mask vectors are then measured in order to compute a fractional Hamming Distance as the measure of the dissimilarity between any two irises, whose two phase code bit vectors are denoted {codeA, codeB} and whose mask bit vectors are denoted {maskA, maskB}:
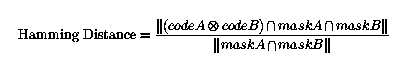
The denominator tallies the total number of phase bits that mattered in iris comparisons after artifacts such as eyelashes and specular reflections were discounted, so the resulting Hamming Distance is a fractional measure of dissimilarity; 0 would represent a perfect match. The Boolean operators XOR and AND are applied in vector form to binary strings of length up to the word length of the CPU, as a single machine instruction. Thus for example on an ordinary 32-bit machine, any two integers between 0 and 4 billion can be XOR'ed in a single machine instruction to generate a third such integer, each of whose bits in a binary expansion is the XOR of the corresponding pair of bits of the original two integers. This implementation of the Hamming Distance computation in parallel 32-bit chunks enables extremely rapid comparisons of IrisCodes when searching through a large database to find a match. On a single 300 MHz CPU, such exhaustive searches are performed at a rate of about 100,000 irises per second. On a single 3 GHz server, one million IrisCodes can be compared in about 1 second.
Search speed scales linearly
with clock frequency, apart from I/O overheads, and of course the search
process is intrinsically parallelizable. Thus databases which may contain
millions of IrisCodes can be farmed into parallel chunks, each managed
by a suitable single CPU, to maintain the desired response speed.