It is important to establish and to measure the amount of independent variation both within an iris and between different irises. There are correlations within an iris because local structure is self-predicting; for example, furrows tend to propagate themselves radially. Such self correlations limit the number of degrees of freedom within irises. But even more important is the question of whether systematic correlations exist between different irises.
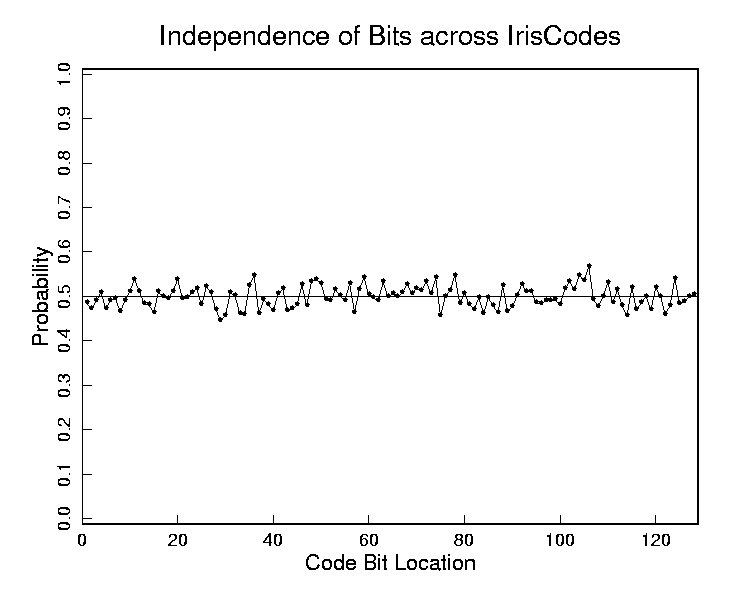
This probability distribution suggests that they do not. It plots the probability that bits in different positions within the IrisCode are set to 1, for a randomly sampled population of different IrisCodes.
The fact that this distribution hovers near 0.5 indicates that all IrisCode bits are equally likely to be 0 or 1. This property makes IrisCodes "maximum entropy" codes in a bit-wise sense. The fact that this distribution is uniform indicates that different irises do not systematically share any common structure. For example, if most irises had a furrow or crypt in the 12-o'clock position, then the plot shown here would not be flat.
The recognition of persons by their IrisCodes is based upon the failure of a test of statistical independence. The plot shown here illustrates why any given IrisCode is "statistically guaranteed" to pass a test of independence against any IrisCode computed from a different eye.