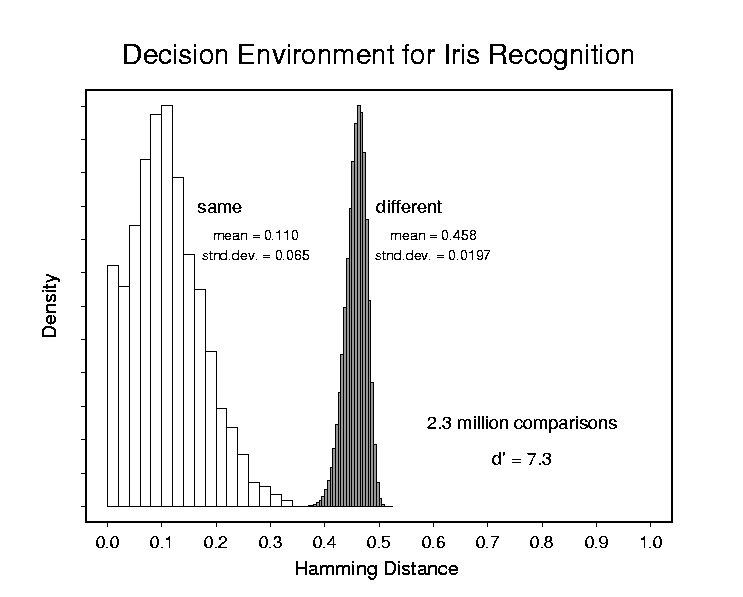
One metric for "decidability," or decision-making power, is d'. This is defined as the separation between the means of the two distributions, divided by the square-root of their average variance. One advantage of using d' for comparing the decision-making power of biometrics is the fact that it does not depend on any choice about the decision threshold used, which of course may vary from liberal to conversative when selecting the trade-off between the False Accept Rate (FAR) and False Reject Rate (FRR). The d' metric is a measure of the inherent degree to which any decrease in one error rate must be paid for by an increase in the other error rate, when decision thresholds are varied. It reflects the intrinsic separability of the two distributions. In an ROC plot [Receiver Operating Characteristic: see scientific papers on this site], d' is related to how "bowed" the ROC curve is. The larger d', the more the ROC reaches into the ideal performance corner, since the two underlying distributions (whose cumulatives the ROC curve plots against each other) are more perfectly separated. This goal of increasing d' (bending the ROC curve more) can be achieved either by pushing further apart the means of the two distributions, or by decreasing their standard deviations, or both.
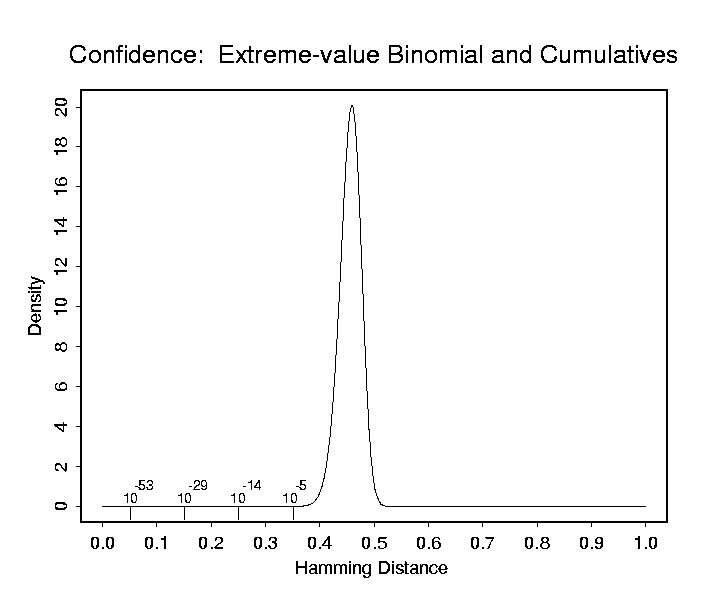
Decidability metrics such as d' can be applied regardless of what measure of similarity a biometric uses. In the particular case of iris recognition, the similarity measure is a Hamming Distance: the fraction of bits in two IrisCodes that disagree. The distribution on the left in the graph shows the results when different images of the same eye are compared; typically about 10% of the bits may differ. But when IrisCodes from different eyes are compared, with rotations to look for and retain the best match (lowest HD), the distribution on the right is the result: the fraction of disagreeing bits is very tightly packed around 45%. Because of the narrowness of this right-hand distribution, which belongs to the family of binomial extreme-value distributions (see scientific papers for mathematical details, and theoretical plot of its probability density function and cumulatives shown below), it is possible to make identification decisions with astronomic levels of confidence. For example, the odds of two different irises agreeing just by chance in more than 75% of their IrisCode bits (i.e. having a Hamming Distance of 0.25 or lower) is only one in 10-to-the-14th power. These extremely low probabilities of getting a False Match enable the iris recognition algorithms to search through extremely large databases, even of a national or planetary (10-to-the-10th) scale, without confusing one IrisCode for another despite so many error opportunities.
A more detailed Technical Report discussing these and other issues related to the
combinatorial complexity of biometric templates, and how this determines
the potential decisiveness of biometric decision-making, is available titled
Biometric Decision Landscapes. (.pdf file)

Back to Main Page.